题目内容
1. 已知Rt△ABC,斜边BC?α,点A∉α,AO⊥α,O为垂足,∠ABO=30°,∠ACO=45°,则二面角A-BC-O的大小为60°.
已知Rt△ABC,斜边BC?α,点A∉α,AO⊥α,O为垂足,∠ABO=30°,∠ACO=45°,则二面角A-BC-O的大小为60°.
分析 过O作OD⊥BC,垂足为D,连结AD,设OC=a,说明∠ADO是二面角A-BC-O的平面角.设AO=a,在Rt△AOD中,求出二面角A-BC-O的大小.
解答 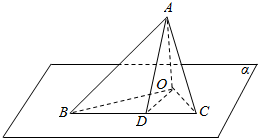 解:如图所示,在平面α内,过O作OD⊥BC,垂足为D,连结AD,设OC=a,
解:如图所示,在平面α内,过O作OD⊥BC,垂足为D,连结AD,设OC=a,
∵AO⊥α,BC?α,∴AO⊥BC.又∵AO∩OD=O,∴BC⊥平面AOD,而AD?平面AOD,
∴AD⊥BC,∴∠ADO是二面角A-BC-O的平面角.
由AO⊥α,OB?α,OC?α可知AO⊥OB,AO⊥OC,又∠ABO=30°,∠ACO=45°,∴设AO=a,则AC=$\sqrt{2}$a,AB=2a,在Rt△ABC中,∠BAC=90°,∴BC=$\sqrt{{AC}^{2}+{AB}^{2}}$=$\sqrt{6}a$,
∴AD=$\frac{AB•AC}{BC}$=$\frac{2a•\sqrt{2}a}{\sqrt{6}a}$=$\frac{2\sqrt{3}}{3}a$.
在Rt△AOD中,sin∠ADO=$\frac{AO}{AD}$=$\frac{a}{\frac{2\sqrt{3}}{3}a}$=$\frac{\sqrt{3}}{2}$,
∴∠ADO=60°,二面角A-BC-O的大小为:60°.
故答案为:60°.
点评 本题考查二面角的平面角的求法,作出二面角的平面角是解题的关键,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
3.不等式$\left\{\begin{array}{l}{3x-2y-2>0}\\{x+4y+4>0}\\{2x+y-6<0}\end{array}\right.$的整数解的个数为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
20.设x,y满足约束条件$\left\{\begin{array}{l}{x-y≥0}\\{x+y-2≥0}\\{x≤4}\end{array}\right.$,当且仅当x=y=4时,z=ax-y取得最小值,则实数a的取值范围是( )
| A. | [-1,1] | B. | (-∞,1) | C. | (0,1) | D. | (-∞,1)∪(1,+∞) |
6.己知A、F分别为双曲线C的左顶点和右焦点,点D在C上,△AFD是等腰直角三角形,且∠AFD=90°,则C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$+1 |
10.函数f(x)=x2-1(x∈R)的值域是( )
| A. | [1,+∞) | B. | (-1,1] | C. | [-1,+∞) | D. | [0,1] |