题目内容
3．不等式$\left\{\begin{array}{l}{3x-2y-2＞0}\\{x+4y+4＞0}\\{2x+y-6＜0}\end{array}\right.$的整数解的个数为（ ）| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
分析 作出不等式所对应的平面区域（如图△ABC内部，不含边界），数形结合可得图中实心点，可得答案．
解答 
解：作出不等式$\left\{\begin{array}{l}{3x-2y-2＞0}\\{x+4y+4＞0}\\{2x+y-6＜0}\end{array}\right.$所对应的平面区域（如图△ABC内部，不含边界），
数形结合可得图中实心点（1，0），（1，-1），（2，0），（2，1），
（2，-1），（3，-1）共6个在区域内部．
故选：D．
点评 本题考查简单线性规划，准确作图是解决问题的关键，属中档题．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
相关题目
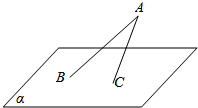如图，平面α的斜线AB交α于B点，且与α所成角为θ，平面α内一动点C满足∠BAC=$\frac{π}{6}$，若动点C的轨迹为椭圆，则θ的取值范围是$\frac{π}{6}$＜θ＜$\frac{π}{2}$．
已知Rt△ABC，斜边BC?α，点A∉α，AO⊥α，O为垂足，∠ABO=30°，∠ACO=45°，则二面角A-BC-O的大小为60°．
2．建立集合A={a，b，c}到集合B={-1，0，1}的映射f：A→B，满足f（a）+f（b）+f（c）=0的不同映射有（ ）
| A． | 6个 | B． | 7个 | C． | 8个 | D． | 9个 |