题目内容
20.设x,y满足约束条件$\left\{\begin{array}{l}{x-y≥0}\\{x+y-2≥0}\\{x≤4}\end{array}\right.$,当且仅当x=y=4时,z=ax-y取得最小值,则实数a的取值范围是( )| A. | [-1,1] | B. | (-∞,1) | C. | (0,1) | D. | (-∞,1)∪(1,+∞) |
分析 作出约束条件$\left\{\begin{array}{l}x-y≥0\\ x+y-2≥0\\ x≤4\end{array}\right.$所对应的可行域,变形目标函数可得y=ax-z,其中直线斜率为a,截距为-z,由题意可得a的范围.
解答  解:作出约束条件$\left\{\begin{array}{l}x-y≥0\\ x+y-2≥0\\ x≤4\end{array}\right.$所对应的可行域(如图阴影),
解:作出约束条件$\left\{\begin{array}{l}x-y≥0\\ x+y-2≥0\\ x≤4\end{array}\right.$所对应的可行域(如图阴影),
变形目标函数可得y=ax-z,其中直线斜率为a,截距为-z,
∵z=ax-y取得最小值的最优解仅为点A(4,4),
∴直线的斜率a<1,
即实数a的取值范围为(-∞,1)
故选:B.
点评 本题考查简单线性规划,准确作图是解决问题的关键,属中档题.

练习册系列答案
相关题目
 已知Rt△ABC,斜边BC?α,点A∉α,AO⊥α,O为垂足,∠ABO=30°,∠ACO=45°,则二面角A-BC-O的大小为60°.
已知Rt△ABC,斜边BC?α,点A∉α,AO⊥α,O为垂足,∠ABO=30°,∠ACO=45°,则二面角A-BC-O的大小为60°.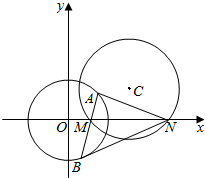 如图,圆C:x2-(1+a)x+y2-ay+a=0.
如图,圆C:x2-(1+a)x+y2-ay+a=0.