题目内容
在▱ABCD中，A(1,1)，
＝(6,0)，点M是线段AB的中点，线段CM与BD交于点P.
(1)若
＝(3,5)，求点C的坐标；
(2)当
时，求点P的轨迹．
解析：(1)设点C坐标为(x0，y0)，
又
＝(3,5)＋(6,0)＝(9,5)，
即(x0－1，y0－1)＝(9,5)，
∴x0＝10，y0＝6，即点C(10,6)．
(2)由三角形相似，不难得出
＝
＝
＝(3(x－1)，3(y－1))－(6,0)
＝(3x－9,3y－3)，
∵
，∴▱ABCD为菱形．
∴AC⊥BD.
∴
，即(x－7，y－1)·(3x－9，3y－3)＝0，
(x－7)(3x－9)＋(y－1)(3y－3)＝0，
∴x2＋y2－10x－2y＋2
2＝0(y≠1)．
∴(x－5)2＋(y－1)2＝4(y≠1)．
∴点P的轨迹是以(5,1
)为圆心，2为半径的圆去掉与直线y＝1的两个交点．
练习册系列答案
天天练口算系列答案
相关题目
B.
＝(cos θ，sin θ)，
＝(2＋sin θ，2－cos θ)，则向量
长度的最大值是________．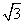
)，b＝(－1,0)，则|a＋2b|＝( )
C．2 D．4
______.