题目内容
7．若函数f（x）=$\left\{\begin{array}{l}{a^x}，（x＞1）\\（4-\frac{a}{2}）x+2，（x≤1）\end{array}$在R上的单调递增，则实数a∈（ ）| A． | （1，+∞） | B． | （1，8） | C． | （4，8） | D． | [4，8） |
分析 利用函数的单调性，可得$\left\{\begin{array}{l}{a＞1}\\{4-\frac{a}{2}＞0}\\{a≥4-\frac{a}{2}+2}\end{array}\right.$，解不等式，即可得出结论．
解答 解：∵函数f（x）=$\left\{\begin{array}{l}{a^x}，（x＞1）\\（4-\frac{a}{2}）x+2，（x≤1）\end{array}$在R上的单调递增，
∴$\left\{\begin{array}{l}{a＞1}\\{4-\frac{a}{2}＞0}\\{a≥4-\frac{a}{2}+2}\end{array}\right.$，∴4≤a＜8，
故选D．
点评 本题考查分段函数的应用，考查函数的单调性，考查计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
7．计算$\underset{lim}{△x→0}$$\frac{sin（\frac{π}{6}+△x）-sin\frac{π}{6}}{△x}$=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | -$\frac{1}{2}$ | D． | -$\frac{\sqrt{3}}{2}$ |
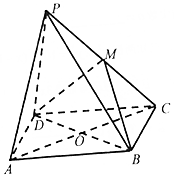如图，点P是菱形ABCD所在平面外一点，∠BAD=60°，△PCD是等边三角形，AB=2，PA=2$\sqrt{2}$，M是PC的中点．