题目内容
17．45弧度是第一象限角．分析 45=（45×$\frac{180}{π}$）°≈2580°=7×360°+60°，是第一象限角，即可得出结论．
解答 解：45=（45×$\frac{180}{π}$）°≈2580°=7×360°+60°，是第一象限角，
故答案为：一．
点评 本题考查弧度与角度的转化，考查象限角，比较基础．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
7．若函数f（x）=$\left\{\begin{array}{l}{a^x}，（x＞1）\\（4-\frac{a}{2}）x+2，（x≤1）\end{array}$在R上的单调递增，则实数a∈（ ）
| A． | （1，+∞） | B． | （1，8） | C． | （4，8） | D． | [4，8） |
12．
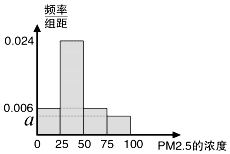根据国家环保部新修订的《环境空气质量标准》规定：居民区PM2.5的年平均浓度不得超过35微克/立方米，PM2.5的24小时平均浓度不得超过75微克/立方米．我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度（单位：微克/立方米）的监测数据，数据统计如表：
（1）将这20天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图．
①求频率分布直方图中a的值；
②求样本平均数，并根据样本估计总体的思想，从PM2.5的年平均浓度考虑，判断该居民区的环境质量是否需要改善？并说明理由．
（2）将频率视为概率，对于2016年的某3天，记这3天中该居民区PM2.5的24小时平均浓度符合环境空气质量标准的天数为X，求X的分布列．
根据国家环保部新修订的《环境空气质量标准》规定：居民区PM2.5的年平均浓度不得超过35微克/立方米，PM2.5的24小时平均浓度不得超过75微克/立方米．我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度（单位：微克/立方米）的监测数据，数据统计如表：| 组别 | PM2.5浓度（微克/立方米） | 频数（天） | 频率 |
| 第一组 | （0，25] | 3 | 0.15 |
| 第二组 | （25，50] | 12 | 0.6 |
| 第三组 | （50，75] | 3 | 0.15 |
| 第四组 | （75，100] | 2 | 0.1 |
①求频率分布直方图中a的值；
②求样本平均数，并根据样本估计总体的思想，从PM2.5的年平均浓度考虑，判断该居民区的环境质量是否需要改善？并说明理由．
（2）将频率视为概率，对于2016年的某3天，记这3天中该居民区PM2.5的24小时平均浓度符合环境空气质量标准的天数为X，求X的分布列．
2．已知x与y之间的一组数据
且x与y的线性回归方程的相关指数R2=1，则m-n=-5．
| x | 0 | 1 | m | 3 |
| y | 1 | 3 | 5 | n |
9．函数$y=2cos（{\frac{1}{2}x+\frac{π}{3}}）$图象的一个对称中心为（ ）
| A． | $（{\frac{4π}{3}，0}）$ | B． | $（{\frac{π}{2}，0}）$ | C． | $（{\frac{π}{3}，0}）$ | D． | $（{\frac{π}{6}，0}）$ |