题目内容
7.计算$\underset{lim}{△x→0}$$\frac{sin(\frac{π}{6}+△x)-sin\frac{π}{6}}{△x}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
分析 利用导数的定义,即可求解.
解答 解:设f(x)=sinx,f′(x)=cosx,
则$\underset{lim}{△x→0}$$\frac{sin(\frac{π}{6}+△x)-sin\frac{π}{6}}{△x}$=cos$\frac{π}{6}$=$\frac{\sqrt{3}}{2}$,
故选B.
点评 本题考查导数的定义,考查学生的计算能力,比较基础.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
2.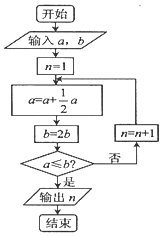 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.下图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的n=( )
宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.下图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的n=( )
 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.下图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的n=( )
宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.下图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的n=( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
19.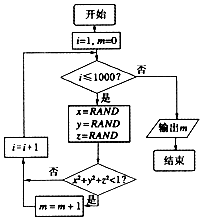 我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为521,则由此可估计π的近似值为( )
我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为521,则由此可估计π的近似值为( )
 我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为521,则由此可估计π的近似值为( )
我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为521,则由此可估计π的近似值为( )| A. | 3.119 | B. | 3.126 | C. | 3.132 | D. | 3.151 |
16.命题“?x∈[1,3],x2≤a”为真命题的一个充分不必要条件是( )
| A. | a≤9 | B. | a≥9 | C. | a≤10 | D. | a≥10 |
7.若函数f(x)=$\left\{\begin{array}{l}{a^x},(x>1)\\(4-\frac{a}{2})x+2,(x≤1)\end{array}$在R上的单调递增,则实数a∈( )
| A. | (1,+∞) | B. | (1,8) | C. | (4,8) | D. | [4,8) |
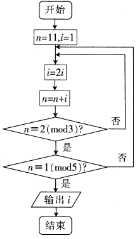 《孙子算经》是中国公元四世纪的数学著作,其中接受了求解依次同余式的方法,他是数论中一个重要的定理,又称《中国剩余定理》,如图所示的程序框图的算法就是源于《中国剩余定理》,执行该程序框图,若正整数N除以正整数m后的余数为n,则记为N≡n(modm),例如11≡3(mod4),则输出的等于( )
《孙子算经》是中国公元四世纪的数学著作,其中接受了求解依次同余式的方法,他是数论中一个重要的定理,又称《中国剩余定理》,如图所示的程序框图的算法就是源于《中国剩余定理》,执行该程序框图,若正整数N除以正整数m后的余数为n,则记为N≡n(modm),例如11≡3(mod4),则输出的等于( )