题目内容
已知各项全不为零的数列{an}的前n项和为Sn，Sn＝
，n∈N*.
(1)求证：数列{an}为等差数列；
(2)若a2＝3，求证：当n∈N*时，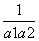
＋
＋…＋
<
.
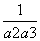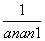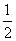证明 (1)由S1＝
＝a1知a1＝1.
当n≥2时，an＝Sn－Sn－1
化简得(n－2)an－(n－1)an－1＋1＝0，①
以n＋1代替n得(n－1)an＋1－nan＋1＝0.②
两式相减得(n－1)an＋1－2(n－1)an＋(n－1)an－1＝0.
则an＋1－2an＋an－1＝0，其中n≥2.
所以，数列{an}为等差数列．
(2)由a1＝1，a2＝3，
结合(1)的结论知an＝2n－1(n∈N*)．
练习册系列答案
相关题目
函数f(x)＝(1－cos x)sin x在[－π，π]的图象大致为( )
满足
当
时，
，则
_______.
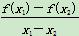≥2，求a的取值范围．
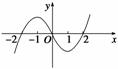设f(x)是一个三次函数，f′(x)为其导函数，如图所示的是y＝x·f′(x)的图象的一部分，则f(x)的极大值与极小值分别是( )
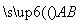＝pm，
＝qn(p>0，q>0)，且满足p＋q＝6时，求△ABC面积的最大值．
，b＝
，c＝
，则( )
，那么
.