题目内容
已知函数f(x)=(a-1)ln x+ax2+1.
(1)讨论函数f(x)的单调性;
(2)如果对任意的x1>x2>0,总有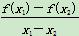 ≥2,求a的取值范围.
≥2,求a的取值范围.
解 (1)f(x)的定义域为(0,+∞),
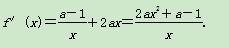 ①当a≥1时,f′(x)>0,故f(x)在(0,+∞)上单调递增;
①当a≥1时,f′(x)>0,故f(x)在(0,+∞)上单调递增;
②当a≤0时,f′(x)<0,故f(x)在(0,+∞)上单调递减;
③当0<a<1时,令f′(x)=0,解得x= 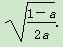
则当x∈(0, 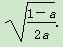 )时,f′(x)<0;
)时,f′(x)<0;
x∈( 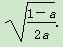 ,+∞)时,f′(x)>0.
,+∞)时,f′(x)>0.
故f(x)在(0, 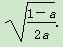 ]上单调递减,
]上单调递减,
在[ 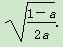 ,+∞)上单调递增.
,+∞)上单调递增.
(2)由已知,可得对任意的x1>x2>0,有x1-x2>0,
所以由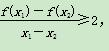 ,
,
得f(x1)-f(x2)≥2(x1-x2),
即f(x1)-2x1≥f(x2)-2x2.
令g(x)=f(x)-2x,又x1>x2,
故函数g(x)=f(x)-2x在(0,+∞)上单调递增.
所以g′(x)=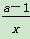 +2ax-2≥0在(0,+∞)上恒成立.
+2ax-2≥0在(0,+∞)上恒成立.
所以(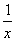 +2x)a≥2+
+2x)a≥2+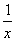 .
.
因为x>0,所以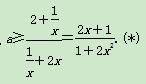
令t=2x+1,则x=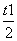 ,
,
又x>0,所以t>1.
故(*)式可化为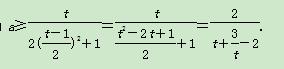 .
.
 即
即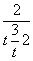 的最大值为
的最大值为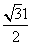 .
.
 故a的取值范围为[
故a的取值范围为[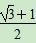 ,+∞).
,+∞).

练习册系列答案
相关题目
 如果存在实数
如果存在实数 使得对任意实数x,都有
使得对任意实数x,都有
 则
则 的最小值是____.
的最小值是____. 为数列
为数列 的前n项和,
的前n项和, 则(1)
则(1) _ ___;
_ ___; __ _..,
__ _.., 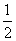 AB,BE=
AB,BE= BC.若
BC.若 (λ1,λ2为实数),则λ1+λ2的值为________.
(λ1,λ2为实数),则λ1+λ2的值为________.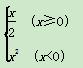 , 则f[f(x)]≥1的充要条件是( )
, 则f[f(x)]≥1的充要条件是( )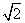 ]
] ,n∈N*.
,n∈N*.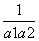 +
+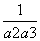 +…+
+…+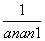 <
<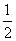 .
. ,则f(2+log23)的值为( )
,则f(2+log23)的值为( ) B.
B.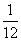 C.
C.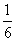 D.
D.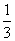
 ,则
,则 ( )
( ) B.
B.  C.
C.  D.
D. 