题目内容
已知圆M:(x+1)2+y2=16及定点N(1,0),点P是圆M上的动点,点Q在线段NP上,点G在线段MP上,且满足
=2
,
•
=0.
(Ⅰ)求点G的轨迹C的方程;
(Ⅱ)是否存在不垂直于坐标轴的直线l和(1)中所求轨迹C相交于不同两点A,B,且满足|NA|=|NB|,若存在,求出直线l的方程;若不存在,说明理由.
| NP |
| NQ |
| GQ |
| NP |
(Ⅰ)求点G的轨迹C的方程;
(Ⅱ)是否存在不垂直于坐标轴的直线l和(1)中所求轨迹C相交于不同两点A,B,且满足|NA|=|NB|,若存在,求出直线l的方程;若不存在,说明理由.
考点:平面向量数量积的运算,直线的一般式方程,轨迹方程
专题:平面向量及应用,圆锥曲线的定义、性质与方程
分析:(I)如图所示,由
=2
,
•
=0可得GQ垂直平分线段NP,可得|GM|+|GN|=|MP|=R=4>|MN|=2.
利用椭圆的定义可得:点G的轨迹C是以M,N为焦点,2a=4为长轴长的椭圆,即可得出.
(II)由于|NA|=|NB|,则A,B两点必定在以N(1,0)为圆心,r为半径的圆上:(x-1)2+y2=r2,而此圆与椭圆都关于x轴对称,其交点AB必定与x轴垂直,即可判断出.
| NP |
| NQ |
| GQ |
| NP |
利用椭圆的定义可得:点G的轨迹C是以M,N为焦点,2a=4为长轴长的椭圆,即可得出.
(II)由于|NA|=|NB|,则A,B两点必定在以N(1,0)为圆心,r为半径的圆上:(x-1)2+y2=r2,而此圆与椭圆都关于x轴对称,其交点AB必定与x轴垂直,即可判断出.
解答:
解:(I)如图所示,∵
=2
,
•
=0.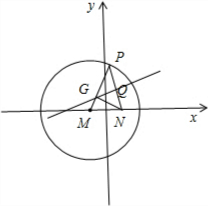
∴Q是线段NP的中点,GQ⊥NP,连接GN.
∴|GN|=|GP|.
∴|GM|+|GN|=|MP|=R=4>|MN|=2.
∴点G的轨迹C是以M,N为焦点,2a=4为长轴长的椭圆,
其方程为:
+
=1.
(II)不存在不垂直于坐标轴的直线l和(I)中所求轨迹C相交于不同两点A,B,且满足|NA|=|NB|.
∵|NA|=|NB|,则A,B两点必定在以N(1,0)为圆心,r为半径的圆上:(x-1)2+y2=r2,而此圆与椭圆都关于x轴对称,其交点AB必定与x轴垂直,
∴不存在不垂直于坐标轴的直线l和(I)中所求轨迹C相交于不同两点A,B,且满足|NA|=|NB|.
| NP |
| NQ |
| GQ |
| NP |

∴Q是线段NP的中点,GQ⊥NP,连接GN.
∴|GN|=|GP|.
∴|GM|+|GN|=|MP|=R=4>|MN|=2.
∴点G的轨迹C是以M,N为焦点,2a=4为长轴长的椭圆,
其方程为:
| x2 |
| 4 |
| y2 |
| 3 |
(II)不存在不垂直于坐标轴的直线l和(I)中所求轨迹C相交于不同两点A,B,且满足|NA|=|NB|.
∵|NA|=|NB|,则A,B两点必定在以N(1,0)为圆心,r为半径的圆上:(x-1)2+y2=r2,而此圆与椭圆都关于x轴对称,其交点AB必定与x轴垂直,
∴不存在不垂直于坐标轴的直线l和(I)中所求轨迹C相交于不同两点A,B,且满足|NA|=|NB|.
点评:本题考查了椭圆的定义及其性质、圆的性质、线段的垂直平分线的性质、向量的共线定理、向量垂直与数量积的关系,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
某程序框图如图所示,该程序运行后输出的k的值是( )


| A、12 | B、13 | C、14 | D、15 |
 某耐磨厂对一批耐磨球的单个重量(单位:克)进行了抽样检测,并绘制出频率分布直方图,已知耐磨球单个重量的范围为[96,106],样本数据分组为[96,98),[98,100),[100,104),[104,106)
某耐磨厂对一批耐磨球的单个重量(单位:克)进行了抽样检测,并绘制出频率分布直方图,已知耐磨球单个重量的范围为[96,106],样本数据分组为[96,98),[98,100),[100,104),[104,106) 如图,动圆D过定点A(0,2),圆心D在抛物线x2=4y上运动,MN为圆D在x轴上截得的弦,当圆心D运动时,记|AM|=m,|AN|=n.
如图,动圆D过定点A(0,2),圆心D在抛物线x2=4y上运动,MN为圆D在x轴上截得的弦,当圆心D运动时,记|AM|=m,|AN|=n. 如图,在三棱柱ABC-A1B1C1中,从顶点A1向底面ABC作垂线,垂足O恰好为AC边的中点,四边形A1ACC1为菱形,且∠A1AC=60°,在△ABC中,AB=BC=
如图,在三棱柱ABC-A1B1C1中,从顶点A1向底面ABC作垂线,垂足O恰好为AC边的中点,四边形A1ACC1为菱形,且∠A1AC=60°,在△ABC中,AB=BC=