题目内容
19.已知|$\overrightarrow{a}$|=5,|$\overrightarrow{b}$|=12,当且仅当m为何值时,向量$\overrightarrow{a}$+m$\overrightarrow{b}$与$\overrightarrow{a}$-m$\overrightarrow{b}$互相垂直.分析 首先由已知向量$\overrightarrow{a}$+m$\overrightarrow{b}$与$\overrightarrow{a}$-m$\overrightarrow{b}$互相垂直得到($\overrightarrow{a}$+m$\overrightarrow{b}$)•($\overrightarrow{a}$-m$\overrightarrow{b}$)=0,展开,得到模长关系式,求出m.
解答 解:若向量$\overrightarrow{a}$+m$\overrightarrow{b}$与$\overrightarrow{a}$-m$\overrightarrow{b}$互相垂直,则有($\overrightarrow{a}$+m$\overrightarrow{b}$)•($\overrightarrow{a}$-m$\overrightarrow{b}$)=0,
∴$\overrightarrow{a}$2-m2$\overrightarrow{b}$2=0.
∵|$\overrightarrow{a}$|=5,|$\overrightarrow{b}$|=12,
∴25-144m 2=0.
∴m=±$\frac{5}{12}$.
∴当且仅当m=±$\frac{5}{12}$时,向量$\overrightarrow{a}$+m$\overrightarrow{b}$与$\overrightarrow{a}$-m$\overrightarrow{b}$互相垂直.
点评 本题考查了平面向量垂直,数量积为0的运用;属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.$\sqrt{si{n}^{2}480°}$等于( )
| A. | ±$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
9.若θ是第一象限角,tanθ=$\frac{3}{4}$,则sinθ等于( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{4}$ |
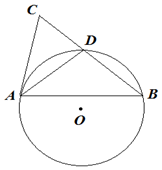 如图,AB和AC分别是⊙O的弦和切线,A为切点,AD为∠BAC的平分线且交⊙O于D,BD的延长线与AC交于C,若AC=6,AD=5,则AB=7.5.
如图,AB和AC分别是⊙O的弦和切线,A为切点,AD为∠BAC的平分线且交⊙O于D,BD的延长线与AC交于C,若AC=6,AD=5,则AB=7.5.