题目内容

11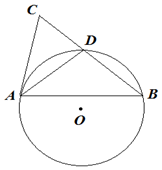．如图，AB和AC分别是⊙O的弦和切线，A为切点，AD为∠BAC的平分线且交⊙O于D，BD的延长线与AC交于C，若AC=6，AD=5，则AB=7.5．

分析 根据切割线定理求出CD，根据角平分线的性质，可得AB．

解答 解：∵AD平分∠BAC
∴∠CAD=∠BAD
∵AC是⊙O的切线
∴∠CAD=∠B（弦切角等于它夹的弧所对的圆周角）
∴∠BAD=∠B
∴BD=AD=5
根据切割线定理AC×AC=CD×BC=CD×（CD+BD）
6×6=CD×CD+5CD
解得CD=4，
根据角平分线的性质，可得$\frac{AB}{6}=\frac{5}{4}$，∴AB=7.5．
故答案为7.5．

点评 本题考查圆的切线的性质，考查切割线定理、角平分线的性质，属于中档题．

练习册系列答案
相关题目
1．已知椭圆$\frac{x^2}{25}+\frac{y^2}{b^2}$=1（0＜b＜5）的离心率$\frac{4}{5}$，则b的值等于（　　）
A．1B．3C．6D．8
2．对某种品牌的灯泡进行寿命跟踪调查，统计如下：
寿命（h）100～200200～300300～400400～500500～600
个数32030804030
（Ⅰ）列出频率分布表；
（Ⅱ）画出频率分布直方图；
（Ⅲ）求灯泡寿命在100h～400h的频率．
19．已知|$\overrightarrow{a}$|=5，|$\overrightarrow{b}$|=12，当且仅当m为何值时，向量$\overrightarrow{a}$+m$\overrightarrow{b}$与$\overrightarrow{a}$-m$\overrightarrow{b}$互相垂直．
6．某商店销售额和利润额如表：
商店名称ABCDE
销售额x（千万元）35679
利润额y（百万元）23345
（1）画出散点图．观察散点图，说明两个变量有怎样的相关性．
（2）计算利润额y对销售额x的回归直线方程．
（3）当销售额为4（千万元）时，估计利润额的大小．
16．在两个变量y与x的回归模型中，分别选择了4个不同模型，它们的相关指数R2如下，其中拟和效果最好的模型是（　　）
A．模型1的相关指数R2为0.25B．模型2的相关指数R2为0.50
C．模型3的相关指数R2为0.98D．模型4的相关指数R2为0.80
3．如图为一个求20个数的平均数的程序，在横线上应填充的语句为（　　）
A．i＞20B．i＜20C．i＞=20D．i＜=20
20．已知一个分段函数可利用函数$S（x）=\left\{\begin{array}{l}1\;，\;x≥0\\ 0\;，\;x＜0\end{array}\right.$来表示，例如要表示一个分段函数$g（x）=\left\{\begin{array}{l}x\;，\;x≥2\\-x\;，\;x＜2\end{array}\right.$，可将函数g（x）表示为g（x）=xS（x-2）+（-x）S（2-x）．现有一个函数f（x）=（-x2+4x-3）S（x-1）+（x2-1）S（1-x）．
（1）求函数f（x）在区间[0，4]上的最大值与最小值；
（2）若关于x的不等式f（x）≤kx对任意x∈[0，+∞）都成立，求实数k的取值范围．
1．在直角坐标平面内，曲线|x-1|+|x+1|+|y|=4围成的图形面积为（　　）
A．12B．16C．20D．24

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网