题目内容

关于x的方程x²+mx+1=0的一个根大于2，另一个根小于2，那么实数m的取值范围是

A.
$数学公式$
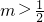
B.
$数学公式$
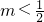
C.
$数学公式$
D.
$数学公式$

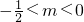
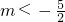
D
分析：设f（x）=x²+mx+1，则由题意可得f（2）=5+2m＜0，由此解得m的范围．
解答：由于关于x的方程x²+mx+1=0的一个根大于2，另一个根小于2，设f（x）=x²+mx+1，
可得f（2）=5+2m＜0，解得m＜- $\text{[math]}$ ，
故选D．
点评：本题主要考查汗水肚饿零点与方程的根的关系，二次函数的性质应用，属于基础题．

练习册系列答案

志鸿优化赢在课堂系列答案

作业辅导系列答案

第一课堂课堂作业系列答案

金牌堂堂练系列答案

一本搞定系列答案

同步学典一课多练系列答案

名师金典BFB初中课时优化系列答案

经典密卷系列答案

启智课堂系列答案

金牌课堂练系列答案

相关题目

若n＞0，关于x的方程x2-(m-2n)x+

mn=0有两个相等的正实数根，求

已知关于x的方程x²+(m+2)x+3=0的两根均大于1，则实数m的取值范围是________.

（本小题满分10分）

已知关于x的方程x²+(m-3)x+m=0

(1)若此方程有实数根，求实数m的取值范围.

(2)若此方程的两实数根之差的绝对值小于,求实数m的取值范围.

若关于x的方程x²+(m-3)x+m=0有两个不相等的正根，求实数m的取值范围.

若关于x的方程x²+(m-3)x+m=0有两个实根，其中一个大于1，另一个小于1，求实数m的取值范围.