题目内容
已知x=lnπ,y=lg3,z=e -
,则( )
| 1 |
| 2 |
| A、x<y<z |
| B、z<x<y |
| C、z<y<x |
| D、y<z<x |
考点:对数的运算性质
专题:函数的性质及应用
分析:根据对数的图象和性质,分别判定x,y的取值范围即可得到结论.
解答:
解:x=lnπ>1,0<lg3<1,0<e -
<1,
lg3<lg
=
,e -
=
>
=
,
则x>1,0<y<
,
<z<1,
故y<z<x,
故选:D
| 1 |
| 2 |
lg3<lg
| 10 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 | ||
|
| 1 | ||
|
| 1 |
| 2 |
则x>1,0<y<
| 1 |
| 2 |
| 1 |
| 2 |
故y<z<x,
故选:D
点评:本题主要考查函数值的大小比较,根据对数和指数幂的性质是解决本题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
复数
=( )
| i2+i3+i4 |
| 1-i |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
设等比数列{an}的前n项和为Sn,满足an>0,q>1,且a3+a5=20,a2a6=64,则S5=( )
| A、31 | B、36 | C、42 | D、48 |
已知{an}是以1为首项的等比数列,若a7•a11=100,则a9的值是( )
| A、-10 | B、10 |
| C、±10 | D、不确定 |
在△ABC中,若角A、B、C的对边分别是a、b、c,则“a2+c2=b2+ac”,是“A、B、C依次成等差数列”的( )
| A、既不充分也不必要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、充要条件 |
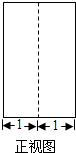 三棱柱的侧棱与底面垂直,且底面是边长为2的等边三角形,其正视图(如图所示)的面积为8,则该三棱柱左视图的面积为( )
三棱柱的侧棱与底面垂直,且底面是边长为2的等边三角形,其正视图(如图所示)的面积为8,则该三棱柱左视图的面积为( )A、2
| ||||
B、
| ||||
C、4
| ||||
D、8
|