题目内容
3.从焦点为F的抛物线y2=2px(p>0)上取一点A(x0,y0)(x0>$\frac{p}{2}$)作其准线的垂线,垂足为B,若|AF|=4,B到直线AF的距离为$\sqrt{7}$,则此抛物线的方程为y2=2x.分析 设B到直线AF的距离为BC=$\sqrt{7}$,求出cos∠BAF=$\frac{3}{4}$,设F到AB的距离为AD,则|AD|=|AF|cos∠BAF=3,即可得出结论.
解答 解:设B到直线AF的距离为BC=$\sqrt{7}$,
由|AF|=|AB|=4,可得sin∠BAF=$\frac{\sqrt{7}}{4}$,
∴cos∠BAF=$\frac{3}{4}$,
设F到AB的距离为AD,则|AD|=|AF|cos∠BAF=3,∴p+|AD|=4,
∴p=1,
∴此抛物线的方程为y2=2x.
故答案为y2=2x.
点评 本题考查抛物线的方程与性质,考查学生的计算能力,属于中档题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
18.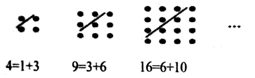 古希腊著名的毕达哥拉斯学派把1、3、6、10、15、…这样的数称为“三角形数”,而把1、4、9、16、25、…这样的数称为“正方形数”.从如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和,下列等式中,符合这一规律的是( )
古希腊著名的毕达哥拉斯学派把1、3、6、10、15、…这样的数称为“三角形数”,而把1、4、9、16、25、…这样的数称为“正方形数”.从如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和,下列等式中,符合这一规律的是( )
 古希腊著名的毕达哥拉斯学派把1、3、6、10、15、…这样的数称为“三角形数”,而把1、4、9、16、25、…这样的数称为“正方形数”.从如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和,下列等式中,符合这一规律的是( )
古希腊著名的毕达哥拉斯学派把1、3、6、10、15、…这样的数称为“三角形数”,而把1、4、9、16、25、…这样的数称为“正方形数”.从如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和,下列等式中,符合这一规律的是( )| A. | 16=3+13 | B. | 25=9+16 | C. | 36=10+26 | D. | 49=21+28 |
8.如图四个散点图中,适合用线性回归模型拟合其中两个变量的是( )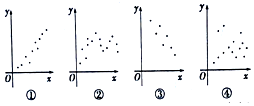

| A. | ①② | B. | ①③ | C. | ②③ | D. | ③④ |
15.已知某批零件的长度误差(单位:毫米)服从正态分布N(0,22),从中随机取一件,其长度误差落在区间(2,4)内的概率为( )(若随机变量ξ服从正态分布N(μ,σ2),则P(μ-σ<ξ<μ+σ)=68.26%,P(μ-2σ<ξ<μ+2σ)=95.44%)
| A. | 4.56% | B. | 13.59% | C. | 27.18% | D. | 31.74% |
12.若i是虚数单位,复数$\frac{1-2i}{i}$的虚部为( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
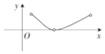
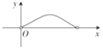

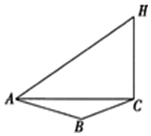 某烟花厂家为了测试最新研制出的一种“冲天”产品升空的安全性,特对其进行了一项测试.如图,这种烟花在燃放点C进行燃放实验,测试人员甲、乙分别在A,B两地(假设三地在同一水平面上),测试人员甲测得A、B两地相距80米且∠BAC=60°,甲听到烟花燃放“冲天”时的声音的时间比乙晚$\frac{1}{17}$秒.在A地测得该烟花升至最高点H处的仰角为60°.(已知声音的传播速度为340米∕秒)
某烟花厂家为了测试最新研制出的一种“冲天”产品升空的安全性,特对其进行了一项测试.如图,这种烟花在燃放点C进行燃放实验,测试人员甲、乙分别在A,B两地(假设三地在同一水平面上),测试人员甲测得A、B两地相距80米且∠BAC=60°,甲听到烟花燃放“冲天”时的声音的时间比乙晚$\frac{1}{17}$秒.在A地测得该烟花升至最高点H处的仰角为60°.(已知声音的传播速度为340米∕秒)