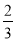题目内容
(本小题满分12分)如图,直三棱柱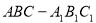 ,底面
,底面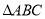 中,
中,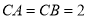 ,
,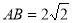 ,棱
,棱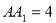 ,
,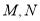 分别是
分别是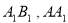 的中点.
的中点.
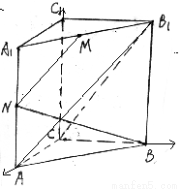
(1)求证: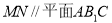 ;
;
(2)求直线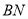 与平面
与平面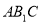 所成的角的正弦值.
所成的角的正弦值.
(1)详见解析;(2)
【解析】
试题分析:(1)因为 分别是
分别是 的中点,所以
的中点,所以 ,所以由线面平行定理可得
,所以由线面平行定理可得 ;(2)以
;(2)以 为原点,分别以
为原点,分别以 所在直线为
所在直线为 轴建立如图的空间直角坐标系,求出平面
轴建立如图的空间直角坐标系,求出平面 的法向量,再利用直线
的法向量,再利用直线 与平面
与平面 的法向量所成角与直线
的法向量所成角与直线 与平面
与平面 所成的角的关系,即可求出直线
所成的角的关系,即可求出直线 与平面
与平面 所成的角.
所成的角.
试题解析:(1) 分别是
分别是 的中点.∴
的中点.∴ ,又因为
,又因为 ∴
∴ 4分
4分
(2)由 ,
, ,得
,得 ,即
,即
∴以 为原点,分别以
为原点,分别以 所在直线为
所在直线为 轴建立如图的空间直角坐标系
轴建立如图的空间直角坐标系 ,
, ,
, ,
, ,
, ,
,
设平面 的法向量
的法向量 ,则
,则 ,取
,取
设直线 与平面
与平面 所成的角为
所成的角为 ,∴
,∴ ,
,
故直线 与平面
与平面 所成的角的正弦值是
所成的角的正弦值是 . 12分
. 12分
考点:(1)线面平行;(2)求线面交.

练习册系列答案
相关题目
 记
记
 的通项公式及数列
的通项公式及数列 的前n项和
的前n项和

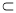 α D.b∥α或b
α D.b∥α或b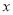 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线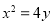 的焦点,离心率
的焦点,离心率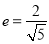 .
.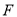 作与坐标轴不垂直的直线
作与坐标轴不垂直的直线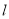 ,交椭圆于
,交椭圆于 、
、 两点,设点
两点,设点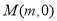 是线段
是线段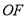 上的一个动点,且
上的一个动点,且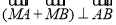 ,求
,求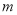 的取值范围;
的取值范围;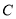 是点
是点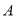 关于
关于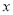 轴的对称点,在
轴的对称点,在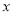 轴上是否存在一个定点
轴上是否存在一个定点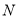 ,使得
,使得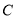 、
、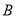 、
、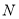 三点共线?若存
三点共线?若存 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.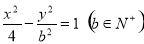 的两个焦点为
的两个焦点为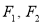 ,
,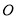 为坐标原点,点
为坐标原点,点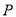 在双曲线上,且
在双曲线上,且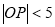 ,若
,若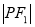 、
、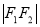 、
、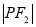 成等比数列,则
成等比数列,则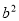 等于( )
等于( )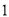 B.
B.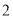 C.
C. D.
D.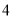
 ( )
( )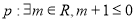 ,命题
,命题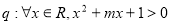 .若“
.若“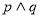 ”为假命题,则实数
”为假命题,则实数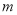 的取值范围是( )
的取值范围是( )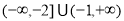 B.
B.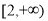
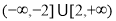 D.
D.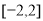
 中,O是底面ABCD的中心,E、F分别是
中,O是底面ABCD的中心,E、F分别是 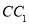 、AD的中点,那么异面直线OE和
、AD的中点,那么异面直线OE和 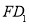 所成角的余弦值等于
所成角的余弦值等于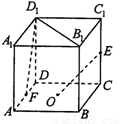
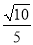 (B).
(B).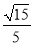
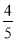 (D)
(D)