题目内容
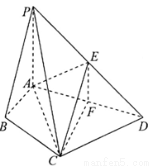
(满分13分)为了绿化城市,准备在如图所示的区域内修建一个矩形PQRC的草坪,且PQ∥BC,RQ⊥BC,另外△AEF的内部有一文物保护区不能占用,经测量AB=100m,BC=80m,AE=30m,AF=20m.

(1)求直线EF的方程.
(2)应如何设计才能使草坪的占地面积最大?
(1) ;(2)当点
;(2)当点 时,S有最大值
时,S有最大值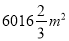 .
.
【解析】
试题分析:(1)建立坐标系,利用直线方程的两点式写出直线方程,化成一般式即可;(2)设出点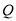 的坐标,进而表示矩形
的坐标,进而表示矩形 的面积表达式,利用二次函数求最值.
的面积表达式,利用二次函数求最值.
解题思路: 解决与解析几何有关的数学实际应用题的关键,合理建立直角坐标系与设出未知量,进而写出有关表达式或等量关系,再利用函数的性质进行求解.
试题解析:(1)建立坐标系如图所示,在线段EF上任取一点Q,分别向BC,CD作垂线.
由题意,直线EF的方程为: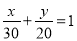 ,即
,即 ;
;
(2)设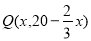 ,则矩形PQRC的面积为:
,则矩形PQRC的面积为: (其中
(其中 );
);
化简,得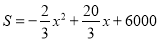 (其中
(其中 );
);
所以,当 时,此时
时,此时 ,即取点
,即取点 时,S有最大值,最大值为
时,S有最大值,最大值为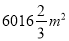 .
.
考点:1.直线方程的两点式;2二次函数的最值.

练习册系列答案
相关题目
 =
= ,且
,且 是第四象限的角,那么
是第四象限的角,那么 =______________
=______________ 中
中 的对边分别为
的对边分别为 若
若 且
且 ,则
,则 ( )
( )  C.4—
C.4—
 中,
中, .若
.若 分别为线段
分别为线段 ,
, 的中点,则直线
的中点,则直线 与平面
与平面 所成角的正弦值为( )
所成角的正弦值为( )
 B.
B. C.
C. D.
D.
 与
与 互相垂直,则a等于( )
互相垂直,则a等于( ) D.1或-3
D.1或-3 过定点 ( )
过定点 ( )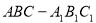 ,底面
,底面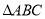 中,
中,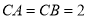 ,
,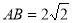 ,棱
,棱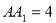 ,
,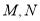 分别是
分别是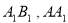 的中点.
的中点.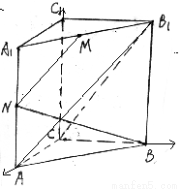
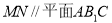 ;
;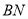 与平面
与平面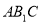 所成的角的正弦值.
所成的角的正弦值.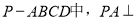 平面ABCD,
平面ABCD,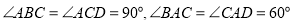 ,E为PD的中点,F在AD上且
,E为PD的中点,F在AD上且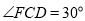 .
.