题目内容
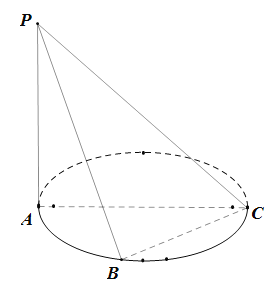
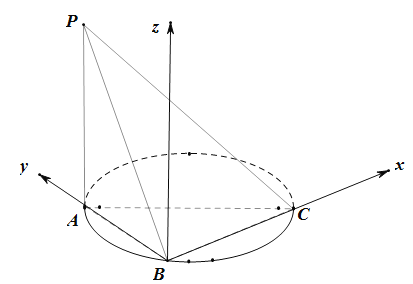
【题目】如图，圆的直径
，
为圆周上不与点
重合的点，
垂直于圆所在的平面，
．
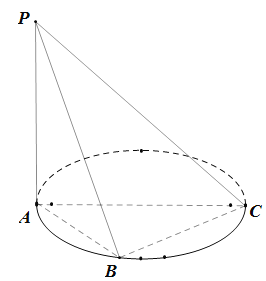
（1）求证：
；
（2）若
，求二面角
的余弦值．
【答案】（1）见解析（2）
【解析】
（1）结合线面垂直的性质得出线线垂直，再利用线面垂直的判定定理得出线线垂直即可．
（2）建立空间直角坐标系，求出各个点的坐标以及向量的坐标，找到平面
的一个法向量，利用向量垂直的性质再结合向量的数量积运算公式求出两个法向量的夹角的余弦值即可得出两个平面所成的角的余弦值．
解：（1）如图，连结
，
因为
平面
，所以
．
又因为
在圆周上，所以
．
又因为
平面
， 
平面，
故
平面．
又
平面．
故
．
（2）因为
，所以可以以
，
为
轴建立如图直角坐标系
则
，
，
，
，
．
平面的一个法向量
．
设平面
的一个法向量
．
则
，
，得
，
取
，得
．
故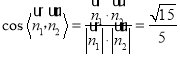
．
活力课时同步练习册系列答案
【题目】某城市美团外卖配送员底薪是每月1800元，设每月配送单数为X，若
，每单提成3元，若
，每单提成4元，若
，每单提成4.5元，饿了么外卖配送员底薪是每月2100元，设每月配送单数为Y,若
，每单提成3元，若
，每单提成4元，小想在美团外卖和饿了么外卖之间选择一份配送员工作，他随机调查了美团外卖配送员甲和饿了么外卖配送员乙在2019年4月份（30天）的送餐量数据，如下表：
表1：美团外卖配送员甲送餐量统计
日送餐量x（单） | 13 | 14 | 16 | 17 | 18 | 20 |
天数 | 2 | 6 | 12 | 6 | 2 | 2 |
表2：饿了么外卖配送员乙送餐量统计
日送餐量x（单） | 11 | 13 | 14 | 15 | 16 | 18 |
天数 | 4 | 5 | 12 | 3 | 5 | 1 |
（1）设美团外卖配送员月工资为
，饿了么外卖配送员月工资为
，当
时，比较 与的大小关系
（2）将4月份的日送餐量的频率视为日送餐量的概率
（ⅰ）计算外卖配送员甲和乙每日送餐量的数学期望E（X）和E（Y）
（ⅱ）请利用所学的统计学知识为小王作出选择，并说明理由．
【题目】某动漫影视制作公司长期坚持文化自信，不断挖掘中华优秀传统文化中的动漫题材，创作出一批又一批的优秀动漫影视作品，获得市场和广大观众的一致好评，同时也为公司赢得丰厚的利润.该公司
年至
年的年利润
关于年份代号
的统计数据如下表（已知该公司的年利润与年份代号线性相关）.
年份 |
|
|
|
|
|
|
|
年份代号 |
|
|
|
|
|
|
|
年利润 |
|
|
|
|
|
|
|
（Ⅰ）求关于的线性回归方程，并预测该公司
年（年份代号记为
）的年利润；
（Ⅱ）当统计表中某年年利润的实际值大于由（Ⅰ）中线性回归方程计算出该年利润的估计值时，称该年为
级利润年，否则称为
级利润年.将（Ⅰ）中预测的该公司年的年利润视作该年利润的实际值，现从年至年这年中随机抽取
年，求恰有
年为级利润年的概率.
参考公式：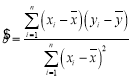
，
.