题目内容
设函数f(x)(x∈R)为奇函数,f(1)=
,f(x+2)=f(x)+f(2),则f(5)= .
| 1 |
| 2 |
考点:抽象函数及其应用
专题:计算题,函数的性质及应用
分析:利用奇函数的定义、函数满足的性质转化求解函数在特定自变量处的函数值是解决本题的关键.利用函数的性质寻找并建立所求的函数值与已知函数值之间的关系,用到赋值法.
解答:
解:由f(1)=
,
对f(x+2)=f(x)+f(2),
令x=-1,
得f(1)=f(-1)+f(2).
又∵f(x)为奇函数,
∴f(-1)=-f(1).
于是f(2)=2f(1)=1;
令x=1,得f(3)=f(1)+f(2)=
,
于是f(5)=f(3)+f(2)=
.
故答案为:
.
| 1 |
| 2 |
对f(x+2)=f(x)+f(2),
令x=-1,
得f(1)=f(-1)+f(2).
又∵f(x)为奇函数,
∴f(-1)=-f(1).
于是f(2)=2f(1)=1;
令x=1,得f(3)=f(1)+f(2)=
| 3 |
| 2 |
于是f(5)=f(3)+f(2)=
| 5 |
| 2 |
故答案为:
| 5 |
| 2 |
点评:本题考查抽象函数求值的方法,考查函数性质在求函数值中的应用,考查了抽象函数求函数值的赋值法.灵活运用已知条件赋值是迅速解决本题的关键,考查学生的转化与化归思想.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
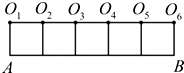 如图,在5个并排的正方形图案中作出一个∠AOnB=135°(n=1,2,3,4,5,6),则n=( )
如图,在5个并排的正方形图案中作出一个∠AOnB=135°(n=1,2,3,4,5,6),则n=( )| A、1,6 | B、2,5 |
| C、3,4 | D、2,3,4,5 |
等差数列{an}中,d=-3,a7=10,则a1等于( )
| A、-39 | B、28 | C、39 | D、32 |
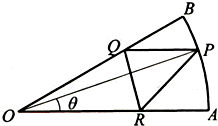 如图,已知扇形AOB是半径为2,圆心角为
如图,已知扇形AOB是半径为2,圆心角为