题目内容
16.已知$\overrightarrow{a}$,$\overrightarrow{b}$是单位向量,且夹角为60°,若向量$\overrightarrow{p}$满足|$\overrightarrow{a}$-$\overrightarrow{b}$-$\overrightarrow{p}$|=$\frac{1}{2}$,则|$\overrightarrow{p}$|的最大值为$\frac{3}{2}$.分析 由题意可设$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),$\overrightarrow{p}$=(x,y),可得(x-$\frac{1}{2}$)2+(y+$\frac{\sqrt{3}}{2}$)2=$\frac{1}{4}$,故向量$\overrightarrow{p}$的终点在以C($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$)为圆心,半径等于$\frac{1}{2}$的圆上,由图象即可得到最大值为|OA|.
解答 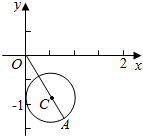 解:$\overrightarrow{a}$,$\overrightarrow{b}$是单位向量,且夹角为60°,
解:$\overrightarrow{a}$,$\overrightarrow{b}$是单位向量,且夹角为60°,
设$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),$\overrightarrow{p}$=(x,y)
则$\overrightarrow{a}$-$\overrightarrow{b}$-$\overrightarrow{p}$=($\frac{1}{2}$-x,-$\frac{\sqrt{3}}{2}$-y),
∵|$\overrightarrow{a}$-$\overrightarrow{b}$-$\overrightarrow{p}$|=$\frac{1}{2}$,即(x-$\frac{1}{2}$)2+(y+$\frac{\sqrt{3}}{2}$)2=$\frac{1}{4}$,
故向量$\overrightarrow{p}$的终点在以C($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$)为圆心,半径等于$\frac{1}{2}$的圆上,
∴|$\overrightarrow{p}$|的最大值为|OA|=|OC|+r=1+$\frac{1}{2}$=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题主要考查两个向量的数量积的运算,熟练掌握向量的坐标运算和圆的方程及数形结合是解题的关键,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 充分非必要条件 | B. | 必要非充分 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
| A. | 32 | B. | 64 | C. | 128 | D. | 256 |
| A. | 3900万次 | B. | 4800万次 | C. | 5070万次 | D. | 6591万次 |