题目内容
已知函数f(x)=sin(x-
)+
cosx,x∈R.
(Ⅰ)求函数f(x)的最小正周期及单调递增区间;
(Ⅱ)在△ABC中,设内角A,B,C所对的边分别为a,b,c.若f(A)=
且a=
b,试求角B的大小.
| π |
| 3 |
| 3 |
(Ⅰ)求函数f(x)的最小正周期及单调递增区间;
(Ⅱ)在△ABC中,设内角A,B,C所对的边分别为a,b,c.若f(A)=
| ||
| 2 |
| ||
| 2 |
考点:三角函数中的恒等变换应用,正弦函数的图象,正弦定理
专题:三角函数的图像与性质
分析:(Ⅰ)将函数f(x)进行化简,利用三角函数的图象和性质即可求函数f(x)的最小正周期及单调递增区间;
(Ⅱ)由f(A)=
求出A的大小,根据a=
b结合正弦定理即可求出B.
(Ⅱ)由f(A)=
| ||
| 2 |
| ||
| 2 |
解答:
解:(1)f(x)=sin(x-
)+
cosx=
sinx+
cosx=sin(x+
),
则函数f(x)的最小正周期T=
=π,
由-
+2kπ≤x-
≤
+2kπ,
解得-
+2kπ≤x≤
+2kπ,
即函数的单调递增区间为[-
+2kπ,
+2kπ],k∈Z.
(2)∵若f(A)=
,
∴sin(A+
)=
,
∵0<A<π,则
<A+
<
,
∴A+
=
,解得A=
,
∵a=
b,
∴
=
=
,即sinB=1,
则B=
.
| π |
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
则函数f(x)的最小正周期T=
| 2π |
| 2 |
由-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
解得-
| π |
| 6 |
| 5π |
| 6 |
即函数的单调递增区间为[-
| π |
| 6 |
| 5π |
| 6 |
(2)∵若f(A)=
| ||
| 2 |
∴sin(A+
| π |
| 3 |
| ||
| 2 |
∵0<A<π,则
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
∴A+
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
∵a=
| ||
| 2 |
∴
| sinA |
| sinB |
| a |
| b |
| ||
| 2 |
则B=
| π |
| 2 |
点评:本题主要考查三角函数的图象和性质,利用辅助角公式将函数进行化简是解决本题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
某程序框图如图所示,则输出的结果S=( )
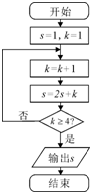

| A、11 | B、26 | C、57 | D、120 |
当x,y满足
时,则t=x+y的最大值是( )
|
| A、1 | B、2 | C、6 | D、5 |
不等式x2+2014x-2015>0的解集为( )
| A、{x|-2015<x<1} |
| B、{x|x>1或x<-2015} |
| C、{x|-1<x<2015} |
| D、{x|x<-1或x>2015} |
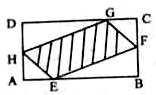 廊坊市某所中学有一块矩形空地,学校要在这块空地上修建一个内接四边形的花坛(如图所示),该花坛的四个顶点分别落在矩形的四条边上,已知 A B=a(a>2),BC=2,且 A E=A H=CF=CG,设 A E=x,花坛面积为y.
廊坊市某所中学有一块矩形空地,学校要在这块空地上修建一个内接四边形的花坛(如图所示),该花坛的四个顶点分别落在矩形的四条边上,已知 A B=a(a>2),BC=2,且 A E=A H=CF=CG,设 A E=x,花坛面积为y.