题目内容
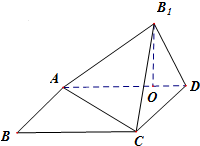 已知四边形ABCD是矩形,AB=1,BC=
已知四边形ABCD是矩形,AB=1,BC=| 3 |
(1)求证:平面AB1C⊥平面B1CD;
(2)求三棱锥B1-ABC的体积VB1-ABC.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)要证面面垂直,需证线面垂直,根据已知,需证AB1⊥面B1CD,然后需证AB1⊥CD,然后再证CD⊥面AB1D,根据面面垂直的性质,不难证明,则将以上过程逆回去,即可证明结论;
(2)根据体积公式,由已知,容易求得△ABC的面积,而高即为B1O,又易证△AB1D为直角△,则斜边AD上的高B1O可求,则体积VB1-ABC-ABC迎刃而解.
(2)根据体积公式,由已知,容易求得△ABC的面积,而高即为B1O,又易证△AB1D为直角△,则斜边AD上的高B1O可求,则体积VB1-ABC-ABC迎刃而解.
解答:
解:(1)∵B1O⊥平面ABCD,CD?平面ABCD,
∴B1O⊥CD,又CD⊥AD,AD∩B1O=O
∴CD⊥平面AB1D,又AB1?平面AB1D
∴AB1⊥CD,又AB1⊥B1C,且B1C∩CD=C
∴AB1⊥平面B1CD,又AB1?平面AB1C
∴平面AB1C⊥平面B1CD.
(2)由于AB1⊥平面B1CD,B1D?平面ABCD,
所以AB1⊥B1D
在Rt△AB1D中,B1D=
=
,
又由B1O•AD=AB1•B1D得B1O=
=
,
所以VB1-ABC=
S△ABC•B1O=
×
×1×
×
=
.
∴B1O⊥CD,又CD⊥AD,AD∩B1O=O
∴CD⊥平面AB1D,又AB1?平面AB1D
∴AB1⊥CD,又AB1⊥B1C,且B1C∩CD=C
∴AB1⊥平面B1CD,又AB1?平面AB1C
∴平面AB1C⊥平面B1CD.
(2)由于AB1⊥平面B1CD,B1D?平面ABCD,
所以AB1⊥B1D
在Rt△AB1D中,B1D=
AD2-A
|
| 2 |
又由B1O•AD=AB1•B1D得B1O=
| AB1•B1D |
| AD |
| ||
| 3 |
所以VB1-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 3 |
| ||
| 6 |
点评:线面的平行、垂直的证明,主要是线线、线面、面面三者之间的平行间关系的转化,垂直间关系的转化,或平行与垂直间的转化,充分体现了转化与化归思想的应用;三棱锥的体积问题,关键是选好底面与高,一般需要变换一下底面与顶点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
①某电话亭内的一部电话1小时内使用的次数记为X;
②某人射击2次,击中目标的环数之和记为X;
③测量一批电阻,阻值在950Ω~1200Ω之间;
④一个在数轴上随机运动的质点,它在数轴上的位置记为X.
其中是离散型随机变量的个数是( )
②某人射击2次,击中目标的环数之和记为X;
③测量一批电阻,阻值在950Ω~1200Ω之间;
④一个在数轴上随机运动的质点,它在数轴上的位置记为X.
其中是离散型随机变量的个数是( )
| A、1 | B、2 | C、3 | D、4 |
数列{an}满足an+1=
,若a1=
,则a2014=( )
|
| 3 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|