题目内容
设函数f(x)=x3-12x+5,x∈R.
(Ⅰ)求f(x)的单调区间和极值;
(Ⅱ)若关于x的方程f(x)=a有3个不同实根,求实数a的取值范围.
(Ⅰ)求f(x)的单调区间和极值;
(Ⅱ)若关于x的方程f(x)=a有3个不同实根,求实数a的取值范围.
考点:根的存在性及根的个数判断,利用导数研究函数的单调性,利用导数研究函数的极值
专题:函数的性质及应用,导数的概念及应用,导数的综合应用
分析:(I)求出函数的导函数,进而分析导函数在不同区间上的符号,进而根据导函数为正,对应函数的单调递增区间;导函数为负,对应函数的单调递减区间,得到f(x)的单调区间;再由左增右减对应函数的极大值,左减右增,对应函数的极小值,得到f(x)的极值;
(II)由(Ⅰ)作出函数f(x)的草图,进而得到方程f(x)=a有3个不同实根,可转化为a值,介于函数的两极值之间,进而得到实数a的取值范围.
(II)由(Ⅰ)作出函数f(x)的草图,进而得到方程f(x)=a有3个不同实根,可转化为a值,介于函数的两极值之间,进而得到实数a的取值范围.
解答:
解:(Ⅰ)∵f(x)=x3-12x+5,
∴f′(x)=3x2-12=3(x+2)(x-2)…(1分)
令f′(x)=0得:x1=-2,x2=2…(2分)
当x变化时,f'(x),f(x)的变化情况如下表:
所以f(x)的增区间是(-∞,-2)和(2,+∞),减区间是(-2,2); …(6分)
当x=-2时,f(x)取得极大值,极大值f(-2)=21; …(7分)
当x=2时,f(x)取得极小值,极小值f(2)=-11.…(8分)
(Ⅱ)由(Ⅰ)得,作出函数f(x)的草图如图所示:
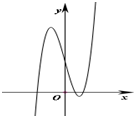
由图可得:
函数的极大值为f(-2)=21,
函数的极大值为f(2)=-11,
则方程f(x)=a有3个不同实根,
可化为函数f(x)的图象与函数y=a的图象有三个交点,
故a∈(-11,21),
所以,实数a的取值范围是(-11,21).…(12分)
∴f′(x)=3x2-12=3(x+2)(x-2)…(1分)
令f′(x)=0得:x1=-2,x2=2…(2分)
当x变化时,f'(x),f(x)的变化情况如下表:
| x | (-∞,-2) | -2 | (-2,2) | 2 | (2,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 增 | 极大 | 减 | 极小 | 增 |
当x=-2时,f(x)取得极大值,极大值f(-2)=21; …(7分)
当x=2时,f(x)取得极小值,极小值f(2)=-11.…(8分)
(Ⅱ)由(Ⅰ)得,作出函数f(x)的草图如图所示:

由图可得:
函数的极大值为f(-2)=21,
函数的极大值为f(2)=-11,
则方程f(x)=a有3个不同实根,
可化为函数f(x)的图象与函数y=a的图象有三个交点,
故a∈(-11,21),
所以,实数a的取值范围是(-11,21).…(12分)
点评:本题考查的知识点是根的存在及根的个数判断,利用导数研究函数的单调性,利用导数研究函数的极值,是函数与导数的综合应用,难度中档.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
函数f(x)=tanx-
在区间(-
,
)内的零点个数是( )
| 1 |
| x |
| π |
| 2 |
| π |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
 已知四边形ABCD是矩形,AB=1,BC=
已知四边形ABCD是矩形,AB=1,BC=