题目内容
已知角α终边上一点P(3,4),求
的值.
cos(
| ||||
cos(
|
考点:运用诱导公式化简求值,任意角的三角函数的定义
专题:三角函数的求值
分析:由条件利用任意角的三角函数的定义求出sinα和cosα的值,再利用诱导公式把要求的式子化为tanα=
,从而求得结果.
| sinα |
| cosα |
解答:
解:∵角α终边上一点P(3,4),∴r=|OP|=5,∴sinα=
=
,cosα=
=
,
∴
=
=
=tanα=
=
=
.
| y |
| r |
| 4 |
| 5 |
| x |
| r |
| 3 |
| 5 |
∴
cos(
| ||||
cos(
|
| -sinα[-sin(π+α)] | ||||
cos(
|
| -sinα•sinα |
| -sinα•cosα |
| sinα |
| cosα |
| ||
|
| 4 |
| 3 |
点评:本题主要考查任意角的三角函数的定义,同角三角函数的基本关系、诱导公式的应用,属于基础题.

练习册系列答案
相关题目
一组数据:1、6、2、2、4、6的中位数为( )
| A、2 | B、3 | C、4 | D、6 |
执行如图所示的程序语句过程中,循环体执行的次数是( )


| A、0 | B、1 | C、2 | D、3 |
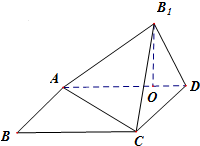 已知四边形ABCD是矩形,AB=1,BC=
已知四边形ABCD是矩形,AB=1,BC=