题目内容
设点 到直线
到直线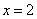 的距离与它到定点
的距离与它到定点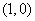 的距离之比为
的距离之比为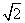 ,并记点
,并记点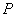 的轨迹为曲线
的轨迹为曲线 .
.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)设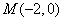 ,过点
,过点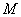 的直线
的直线 与曲线
与曲线 相交于
相交于 两点,当线段
两点,当线段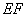 的中点落在由四点
的中点落在由四点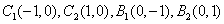 构成的四边形内(包括边界)时,求直线
构成的四边形内(包括边界)时,求直线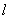 斜率的取值范围.
斜率的取值范围.
解:(Ⅰ)有题意 ,
,
 整理得
整理得 ,所以曲线
,所以曲线 的方程为
的方程为
(Ⅱ)显然直线 的斜率
的斜率 存在,所以可设直线
存在,所以可设直线 的方程为
的方程为 .
.
设点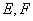 的坐标分别为
的坐标分别为
线段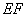 的中点为
的中点为
 ,
,
由
得
由 解得
解得 .…(1)
.…(1)
由韦达定理得 ,于是
,于是
 =
= ,
,
因为 ,所以点
,所以点 不可能在
不可能在 轴的右边,
轴的右边,
又直线 ,方程分别为
,方程分别为
所以点 在正方形内(包括边界)的充要条件为
在正方形内(包括边界)的充要条件为
 即
即 亦即
亦即
解得 ,……………(2)
,……………(2)
由(1)(2)知,直线 斜率的取值范围是
斜率的取值范围是

练习册系列答案
相关题目
 且
且 则二次函数
则二次函数 的零点个数为( )
的零点个数为( ) ,命题
,命题 若命题“
若命题“ ”是真命题,则实数
”是真命题,则实数 的取值范围为 .
的取值范围为 .  的图象可能是
的图象可能是
 的左焦点
的左焦点 ,作圆
,作圆 的切线,切点为E,延长EF交双曲线右支于点P,若E是FP的中点,则双曲线的离心率为____.
的切线,切点为E,延长EF交双曲线右支于点P,若E是FP的中点,则双曲线的离心率为____. 上的最短路程是( )
上的最短路程是( ) D.
D. 
 中,角A,B,C的对边分别为a,b,c,已知
中,角A,B,C的对边分别为a,b,c,已知 ,
, .
. 的值;
的值; 为
为 的中点,求
的中点,求 的长.
的长.