题目内容
12.已知集合A={x|x2-2x+1<a2},B={x|-1<x<2},若A⊆B,则正实数a的取值范围为( )| A. | (1,+∞) | B. | (1,2] | C. | (0,1] | D. | (0,2] |
分析 根据集合的包含关系,列出不等式,求出实数a的取值范围.
解答 解:集合A={x|x2-2x+1<a2}={x|1-a<x<1+a},
∵B={x|-1<x<2},A⊆B,
∴$\left\{\begin{array}{l}{1-a≥-1}\\{1+a≤2}\end{array}\right.$,
∴a≤1,
∵a>0,
∴0<a≤1.
故选:C.
点评 本题主要考查集合的基本运算,属于基础题.要正确判断两个集合间的关系,必须对集合的相关概念有深刻的理解,善于抓住代表元素,认清集合的特征.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
12.已知向量$\overrightarrow a=({1,0})$,$\overrightarrow b=(cosθ,sinθ)$,$θ∈[{-\frac{π}{4},\frac{π}{2}}]$,则$|{\overrightarrow a+\overrightarrow b}|$的取值范围是( )
| A. | $[0,\sqrt{2}]$ | B. | [0,2] | C. | [1,2] | D. | $[\sqrt{2},2]$ |
9.在如图的知识结构图中:“求简单函数的导数”的“上位”要素有( )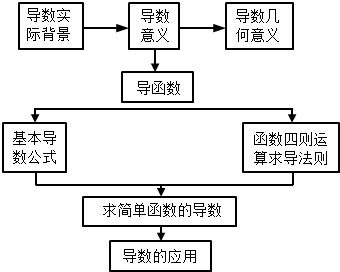

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.等边三角形ABC的边长是a,AD是BC边上的高,沿AD将△ABC折成直二面角,则点B、C的距离是( )
| A. | $\frac{1}{2}$a | B. | $\frac{\sqrt{2}}{2}$a | C. | $\frac{\sqrt{3}}{2}$a | D. | a |
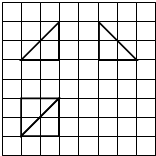 如图所示,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱与底面所成角的正弦值为$\frac{\sqrt{3}}{3}$.
如图所示,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱与底面所成角的正弦值为$\frac{\sqrt{3}}{3}$.