题目内容
若(x2+
)n(n∈N*,n≤100)展开式中一定存在常数项,则n最大值为( )
| 1 |
| x |
| A、90 | B、96 | C、99 | D、100 |
考点:二项式系数的性质
专题:二项式定理
分析:在二项展开式的通项公式中,令x的幂指数等于0,求出 2n=3r,即n是3的倍数,再结合n≤100,求得n的最大值.
解答:
解:(x2+
)n(n∈N*,n≤100)展开式的通项公式为 Tr+1=
x2n-3r,
令2n-3r=0,可得 2n=3r,即n是3的倍数.
再根据n≤100,可得n的最大值为99,
故选:C.
| 1 |
| x |
| C | r n |
令2n-3r=0,可得 2n=3r,即n是3的倍数.
再根据n≤100,可得n的最大值为99,
故选:C.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知变量x、y满足
,则z=2x+y+4最大值为( )
|
| A、16 | B、8 | C、6 | D、4 |
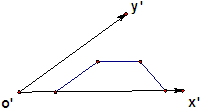 一个水平放置的平面图形的直观图是一个底角为45°,腰和上底长均为1的等腰梯形,则该平面图形的面积等于( )
一个水平放置的平面图形的直观图是一个底角为45°,腰和上底长均为1的等腰梯形,则该平面图形的面积等于( )A、
| ||||||
B、1+
| ||||||
C、1+
| ||||||
D、2+
|
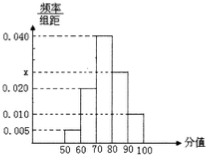 为了全面推进素质教育,教育部门对某省500所中小学进行调研考评,考评分数在80分以上(含80分)的授予“素质教育先进学校”称号,考评统计结果如图的频率分布直方图所示,则应授予“素质教育先进学校”称号的学校有( )所.
为了全面推进素质教育,教育部门对某省500所中小学进行调研考评,考评分数在80分以上(含80分)的授予“素质教育先进学校”称号,考评统计结果如图的频率分布直方图所示,则应授予“素质教育先进学校”称号的学校有( )所.| A、125 | B、175 |
| C、325 | D、50 |
对任意的实数m,直线y=mx+1与圆x2+y2=4的位置关系一定是( )
| A、相切 |
| B、相交且直线过圆心 |
| C、相交且直线不过圆心 |
| D、相离 |
若sinα<0,且tanα<0,则α是( )的角.
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
某程序框图如图所示,则该程序运行后输出的值为( )


| A、23 | B、47 | C、95 | D、191 |