题目内容
已知定义在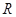 上的奇函数
上的奇函数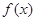 ,当
,当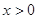 时,
时,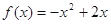
(1)求函数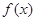 在
在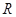 上的解析式;(2)若函数
上的解析式;(2)若函数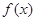 在区间
在区间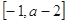 上单调递增,求实数
上单调递增,求实数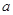 的取值范围。
的取值范围。
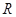 上的奇函数
上的奇函数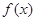 ,当
,当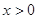 时,
时,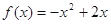
(1)求函数
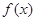 在
在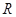 上的解析式;(2)若函数
上的解析式;(2)若函数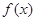 在区间
在区间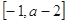 上单调递增,求实数
上单调递增,求实数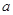 的取值范围。
的取值范围。(1) (2)
(2)
 (2)
(2)
试题分析:(1)因为x>0的解析式去为
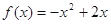 所以可以求x<0的解析式
所以可以求x<0的解析式 函数是奇函数所以f(0)=0综上所述
函数是奇函数所以f(0)=0综上所述 (2)要使f(x)在[-1,a-2]上单调递增.由图像可知
(2)要使f(x)在[-1,a-2]上单调递增.由图像可知 解得不等式为:
解得不等式为: .
.试题解析:(1)设x<0,则-x>0,
 . 3分
. 3分又f(x)为奇函数,所以f(-x)=-f(x).
于是x<0时
 5分
5分所以
 6分
6分(2)要使f(x)在[-1,a-2]上单调递增, (画出图象得2分)
结合f(x)的图象知
 10分
10分所以
 故实数a的取值范围是(1,3]. 12分
故实数a的取值范围是(1,3]. 12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 为实数,
为实数, .
.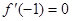 ,求
,求 在
在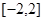 上的最大值和最小值;
上的最大值和最小值;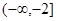 和
和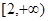 上都是递增的,求
上都是递增的,求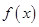 是定义在
是定义在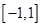 上的奇函数,在
上的奇函数,在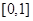 上
上 .
. .
.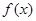 是
是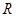 上的奇函数,且当
上的奇函数,且当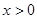 时,
时,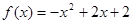 .
.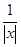 .
.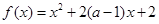 在区间
在区间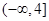 内递减,那么实数
内递减,那么实数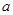 的取值范围为( )
的取值范围为( )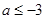
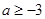
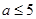
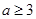
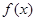 满足
满足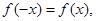 且当
且当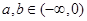 时总有
时总有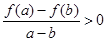 ,其中
,其中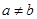 .
. 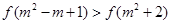 ,则实数
,则实数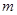 的取值范围是 .
的取值范围是 .