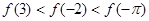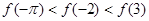题目内容
已函数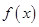 是定义在
是定义在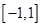 上的奇函数,在
上的奇函数,在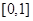 上
上 .
.
(1)求函数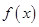 的解析式;并判断
的解析式;并判断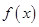 在
在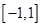 上的单调性(不要求证明);
上的单调性(不要求证明);
(2)解不等式 .
.
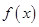 是定义在
是定义在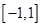 上的奇函数,在
上的奇函数,在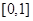 上
上 .
.(1)求函数
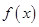 的解析式;并判断
的解析式;并判断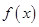 在
在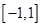 上的单调性(不要求证明);
上的单调性(不要求证明);(2)解不等式
 .
.(1)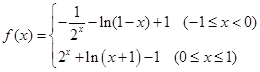 ,
,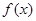 是
是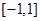 上增函数;(2)不等式的解集为
上增函数;(2)不等式的解集为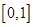 .
.
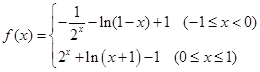 ,
,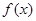 是
是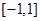 上增函数;(2)不等式的解集为
上增函数;(2)不等式的解集为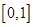 .
.试题分析:(1)这是由函数的对称性求函数的解析式问题,先设
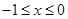 ,进而得到
,进而得到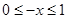 ,根据奇函数的定义即可得出
,根据奇函数的定义即可得出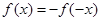
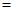
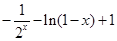 ,从而可写出函数的解析式,对于函数的单调性则根据指数函数、对数函数的单调性及奇函数的性质进行判断即可;(2)先根据奇函数的定义进行化简不等式,转化为
,从而可写出函数的解析式,对于函数的单调性则根据指数函数、对数函数的单调性及奇函数的性质进行判断即可;(2)先根据奇函数的定义进行化简不等式,转化为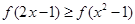 ,进而根据函数的单调性与定义域,列出不等式组
,进而根据函数的单调性与定义域,列出不等式组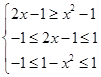 ,从中求解该不等式组即可.
,从中求解该不等式组即可.试题解析:(1)设
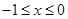 ,则
,则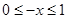
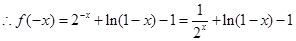
又
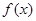 是奇函数,所以
是奇函数,所以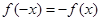 ,
,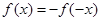
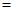
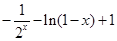 3分
3分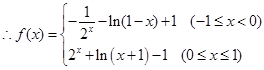
当
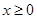 时,
时,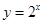 、
、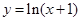 单调递增,所以
单调递增,所以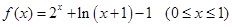 单调递增且
单调递增且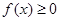 ,由奇函数的性质可知
,由奇函数的性质可知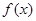 在
在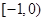 也单调递增且
也单调递增且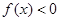
所以
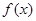 是
是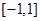 上的增函数
上的增函数(2)
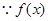 是
是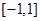 上增函数,由已知得
上增函数,由已知得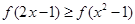
等价于
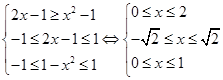
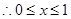
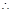 不等式的解集为
不等式的解集为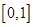 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 上的奇函数
上的奇函数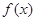 ,当
,当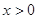 时,
时,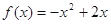
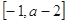 上单调递增,求实数
上单调递增,求实数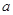 的取值范围。
的取值范围。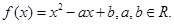
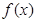 在区间
在区间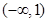 上单调递减,求
上单调递减,求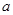 的取值范围;
的取值范围;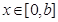 时,
时,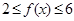 恒成立,求
恒成立,求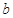 的最大值及此时
的最大值及此时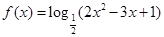 的增区间是____________.
的增区间是____________.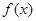 是定义在
是定义在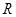 上的奇函数,且
上的奇函数,且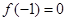 ,若不等式
,若不等式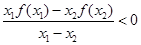 对区间
对区间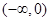 内任意的两个不相等的实数
内任意的两个不相等的实数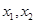 都成立,则不等式
都成立,则不等式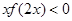 的解集是 。
的解集是 。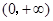 上单调递增的是( )
上单调递增的是( )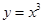
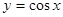
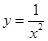
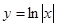
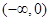 上单调递增的是( )
上单调递增的是( )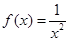
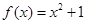
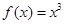
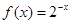
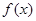 为定义域在R上的偶函数,且
为定义域在R上的偶函数,且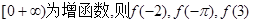 的大小顺序为( )
的大小顺序为( )