题目内容
已知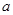 为实数,
为实数, .
.
(1)若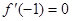 ,求
,求 在
在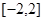 上的最大值和最小值;
上的最大值和最小值;
(2)若 在
在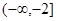 和
和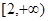 上都是递增的,求
上都是递增的,求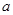 的取值范围.
的取值范围.
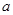 为实数,
为实数, .
.(1)若
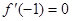 ,求
,求 在
在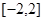 上的最大值和最小值;
上的最大值和最小值;(2)若
 在
在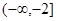 和
和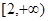 上都是递增的,求
上都是递增的,求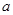 的取值范围.
的取值范围.(1) ,
,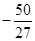 ;(2)
;(2)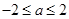 .
.
 ,
,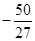 ;(2)
;(2)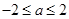 .
.试题分析:解题思路:(1)求导函数,利用
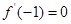 ,解得
,解得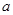 的值;再求最值;(2)利用“若函数
的值;再求最值;(2)利用“若函数 在某区间上单调递增,则
在某区间上单调递增,则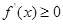 在该区间恒成立”求解.规律总结:(1)求函数最值的步骤:①求导函数;②求极值;③比较极值与端点值,得出最值;(2)若函数
在该区间恒成立”求解.规律总结:(1)求函数最值的步骤:①求导函数;②求极值;③比较极值与端点值,得出最值;(2)若函数 在某区间上单调递增,则
在某区间上单调递增,则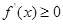 在该区间恒成立;“若函数
在该区间恒成立;“若函数 在某区间上单调递减,则
在某区间上单调递减,则 在该区间恒成立.
在该区间恒成立.试题解析:(1)
 .
.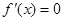 时,
时, 或
或 ,
, 在
在 上单调递增,在
上单调递增,在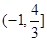 上上单调递减,在
上上单调递减,在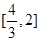 上单调递增;所以
上单调递增;所以 在
在 上的最大值为
上的最大值为 ,最小值为
,最小值为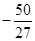 .
.(2)
 的图象为过
的图象为过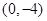 ,开口向上的抛物线由题
,开口向上的抛物线由题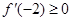 且
且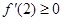 解得
解得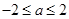 .
.
练习册系列答案
相关题目
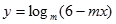 在
在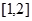 上单调递减.
上单调递减.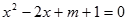 在
在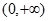 内有一个零点.若p或q为真,p且q为假,求实数m的取值范围.
内有一个零点.若p或q为真,p且q为假,求实数m的取值范围.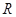 上的奇函数
上的奇函数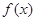 ,当
,当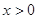 时,
时,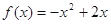
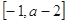 上单调递增,求实数
上单调递增,求实数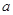 的取值范围。
的取值范围。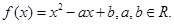
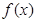 在区间
在区间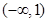 上单调递减,求
上单调递减,求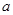 的取值范围;
的取值范围;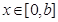 时,
时,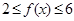 恒成立,求
恒成立,求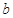 的最大值及此时
的最大值及此时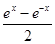 ,x∈R
,x∈R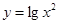 的单调减区间为
的单调减区间为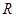
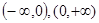

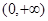
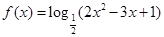 的增区间是____________.
的增区间是____________.