题目内容
11.若集合A={x|${log_{\frac{1}{2}}}(x+1)$>-1},集合B={x|1<3x<9},则(∁RA)∩B=( )| A. | (0,1] | B. | [1,2) | C. | (1,2) | D. | (0,1) |
分析 分别求解对数不等式和指数不等式化简集合A,B,求出∁RA,然后利用交集运算得答案.
解答 解:由${log_{\frac{1}{2}}}(x+1)$>-1=$lo{g}_{\frac{1}{2}}2$,得0<x+1<2,
∴-1<x<1,
则A={x|${log_{\frac{1}{2}}}(x+1)$>-1}=(-1,1),
∴∁RA=(-∞,-1]∪[1,+∞),
又B={x|1<3x<9}=(0,2),
∴(∁RA)∩B=[1,2).
故选:B.
点评 本题考查指数不等式和对数不等式的解法,考查了交、并、补集的混合运算,是基础题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
1.2位男生和3位女生共5位同学站成一排,则3位女生中有且只有两位女生相邻的概率是( )
| A. | $\frac{3}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
2.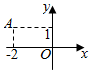 如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$对应的点在( )
如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$对应的点在( )
 如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$对应的点在( )
如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$对应的点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6.(1+x)4的展开式中x2的系数为( )
| A. | 1 | B. | 4 | C. | 6 | D. | 12 |
1.已知函数f(x)=log2(2-ax)在(-∞,1]上是减函数,则a的范围是( )
| A. | [1,2] | B. | (1,2) | C. | (1,+∞) | D. | (-∞,2) |