题目内容
在△ABC中,AB=1,BC=2,CA=
,I是△ABC的内心,则向量
在向量
上的投影为 .
| 3 |
| AI |
| BA |
考点:向量的投影
专题:平面向量及应用
分析:如图所示,设△ABC的内切圆的半径为r,可得
•r(1+2+
)=
×1×
,解得r.利用向量
在向量
上的投影即可得出.
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| AI |
| BA |
解答:
解:如图所示,
设△ABC的内切圆的半径为r,
则
•r(1+2+
)=
×1×
,
解得r=
.
∴
=(
,
),
=(-1,0).
∴向量
在向量
上的投影=
=
=
,
故答案为:
.

设△ABC的内切圆的半径为r,
则
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
解得r=
| ||
| 2 |
∴
| AI |
| ||
| 2 |
| ||
| 2 |
| BA |
∴向量
| AI |
| BA |
| ||||
|
|
| ||||
| 1 |
1-
| ||
| 2 |
故答案为:
1-
| ||
| 2 |
点评:本题考查了三角形内切圆的性质、向量的数量积及其投影,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
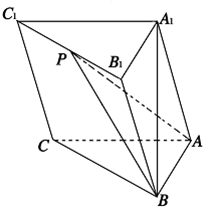 如图,在三棱柱ABC-A1B1C1中,AB⊥AC,AC⊥BB1,AB=A1B=AC=1,BB1=
如图,在三棱柱ABC-A1B1C1中,AB⊥AC,AC⊥BB1,AB=A1B=AC=1,BB1=