题目内容
18.若动点A(x1,y1),B(x2,y2)分别在直线l1:x+y-2=0和l2:x+y-6=0上移动,则AB中点M到原点距离的最小值为( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
分析 设AB中点M(x,y),则$\frac{|x+y-2|}{\sqrt{2}}$=$\frac{|x+y-6|}{\sqrt{2}}$,可得中点所在直线方程:x+y-4=0,则AB中点M到原点距离的最小值为原点到上述直线的距离.
解答 解:设AB中点M(x,y),则$\frac{|x+y-2|}{\sqrt{2}}$=$\frac{|x+y-6|}{\sqrt{2}}$,化为:x+y-4=0,
则AB中点M到原点距离的最小值=$\frac{|0-4|}{\sqrt{2}}$=2$\sqrt{2}$.
故选:A.
点评 本题考查了点到直线的距离公式、相互平行的直线斜率之间的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
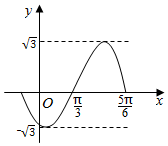 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图所示,则g(x)=f(x)+f($\frac{π}{4}$+x)的单调递增区间是[kπ-$\frac{π}{24}$,kπ+$\frac{11π}{24}$],k∈Z.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图所示,则g(x)=f(x)+f($\frac{π}{4}$+x)的单调递增区间是[kπ-$\frac{π}{24}$,kπ+$\frac{11π}{24}$],k∈Z.