题目内容
9.已知数列{an}满足a1=1,an+1+an=2n+1,求an.分析 由数列递推式可得数列{an}的所有奇数项构成以1为首项,以2为公差的等差数列,偶数项构成以2为首项,以2为公差的等差数列.再由等差数列的通项公式求得答案.
解答 解:由an+1+an=2n+1,得
an+2+an+1=2(n+1)+1=2n+3,
两式作差得an+2-an=2.
又a1=1,得a2=3-a1=2,
∴数列{an}的所有奇数项构成以1为首项,以2为公差的等差数列,
偶数项构成以2为首项,以2为公差的等差数列.
则当n为奇数时,an=1+2($\frac{n+1}{2}$-1)=n
当n为偶数时,an=2+2($\frac{n}{2}$-1)=n,
综上所述an=n
点评 本题考查数列递推式,考查了等差数列通项公式的求法,体现了分类讨论的数学思想方法,是中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
4.F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,过点F作双曲线的一条渐近线的垂线,垂足为A,交另一条渐近线于点B.若3$\overrightarrow{FA}$=$\overrightarrow{FB}$,则此双曲线的离心率为( )
| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
18.若动点A(x1,y1),B(x2,y2)分别在直线l1:x+y-2=0和l2:x+y-6=0上移动,则AB中点M到原点距离的最小值为( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
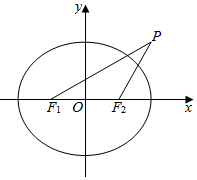 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点为F1,F2,焦距为2,设点P(a,b)满足△PF1F2是等腰三角形.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点为F1,F2,焦距为2,设点P(a,b)满足△PF1F2是等腰三角形.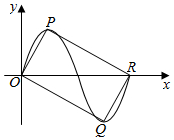 如图,四边形OQRP为矩形,其中P,Q分别是函数f(x)=$\sqrt{3}$sinwx(A>0,w>0)图象上的一个最高点和最低点,O为坐标原点,R为图象与x轴的交点.
如图,四边形OQRP为矩形,其中P,Q分别是函数f(x)=$\sqrt{3}$sinwx(A>0,w>0)图象上的一个最高点和最低点,O为坐标原点,R为图象与x轴的交点.