题目内容
(本小题满分12分,(1)小问5分,(2)小问7分)
已知函数 .
.
(1)设函数 ,若函数
,若函数 为偶函数,求实数
为偶函数,求实数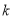 的值;
的值;
(2)当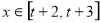 时,是否存在实数
时,是否存在实数 (其中
(其中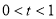 ),使得不等式
),使得不等式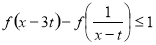 恒成立?若存在,求出
恒成立?若存在,求出 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(1) ;(2)不存在t符合题意
;(2)不存在t符合题意
【解析】
试题分析:(1)∵函数g(x)为偶函数,∴g(-x)=g(x)
∴ ,
,
整理得(2k+1)x=0,∴
(2)不等式 ,等价于
,等价于 恒成立,
恒成立,
即 ,h(x)的对称轴为x=2t,
,h(x)的对称轴为x=2t,
∵0<t<1,∴2t<t+2,
∴函数h(x)在[t+2,t+3]上单调递增,
∴ ,解得
,解得 ,又0<t<1,所以不存在t符合题意.
,又0<t<1,所以不存在t符合题意.
考点:函数的奇偶性,函数恒成立的问题

练习册系列答案
相关题目
 中,点
中,点 分别是
分别是 上的点,将
上的点,将 折起,使
折起,使 两点重合于
两点重合于 .
.
 ;
; 时,
时, 的体积.
的体积.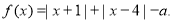
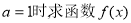 的最小值;
的最小值;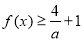 对任意的实数
对任意的实数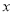 恒成立,求实数
恒成立,求实数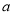 的取值范围.
的取值范围. 的图像大致是( )
的图像大致是( )
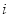 是虚数单位,若复数
是虚数单位,若复数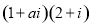 是纯虚数,则实数
是纯虚数,则实数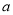 等于( )
等于( )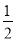 C.
C.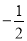 D.
D.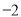
 = .
= .
 ,
, 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, ,则函数
,则函数 的大致图象为( )
的大致图象为( )

 +
+ =1与双曲线
=1与双曲线 -
- =1(m,n,p,q∈R+)有共同的焦点F1、F2,P是椭圆和双曲线的一个交点,则|PF1|·|PF2|= 。
=1(m,n,p,q∈R+)有共同的焦点F1、F2,P是椭圆和双曲线的一个交点,则|PF1|·|PF2|= 。 为偶函数且
为偶函数且 ,又
,又 ,函数
,函数 ,若
,若 恰好有2个零点,则
恰好有2个零点,则 .
.