题目内容
11.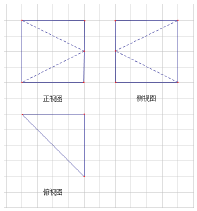 图中,小方格是边长为1的正方形,图中粗线画出的是某几何体的三视图,且该几何体的顶点都在同一球面上,则该几何体的外接球的表面积为( )
图中,小方格是边长为1的正方形,图中粗线画出的是某几何体的三视图,且该几何体的顶点都在同一球面上,则该几何体的外接球的表面积为( )| A. | 32π | B. | 48π | C. | 50π | D. | 64π |
分析 通过还原三视图确定几何体,利用空间中的位置关系计算可得球的半径,进而利用面积公式即得结论.
解答  解:由三视图可知该几何体是一个底面是矩形的四棱锥,
解:由三视图可知该几何体是一个底面是矩形的四棱锥,
记该几何体的外接球球心为O,半径R=OA,
则PA=$\frac{1}{2}$×$\sqrt{{4}^{2}+{4}^{2}+{4}^{2}}$=$2\sqrt{3}$,OP=R-$2\sqrt{3}$,
所以OA2=OP2+AP2,
又因为OP2=$(R-\frac{1}{2}×\sqrt{{4}^{2}+{4}^{2}})^{2}$=$(R-2\sqrt{2})^{2}$,
所以R2=$(R-2\sqrt{2})^{2}$+$(2\sqrt{3})^{2}$,解得:R=$\frac{5}{\sqrt{2}}$,
所以所求面积S=4π×R2=4π×$(\frac{5}{\sqrt{2}})^{2}$=50π,
故选:C.
点评 本题考查三视图求面积,考查空间想象能力,找出球心是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
14.若{an}是等差数列,且a1=-1,公差为-3,则a8等于( )
| A. | -7 | B. | -8 | C. | -22 | D. | 27 |
6.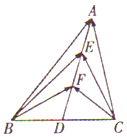 如图.在△ABC中,D是BC的中点,E、F是AD上的两个三等分点,$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BF}$•$\overrightarrow{CF}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是( )
如图.在△ABC中,D是BC的中点,E、F是AD上的两个三等分点,$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BF}$•$\overrightarrow{CF}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是( )
 如图.在△ABC中,D是BC的中点,E、F是AD上的两个三等分点,$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BF}$•$\overrightarrow{CF}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是( )
如图.在△ABC中,D是BC的中点,E、F是AD上的两个三等分点,$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BF}$•$\overrightarrow{CF}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是( )| A. | 4 | B. | 8 | C. | $\frac{7}{8}$ | D. | $\frac{3}{4}$ |
1.已知i是虚数单位,复数z满足z=i(i-1),则z的虚部是( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
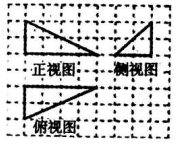 如图,网格纸上的小正方形边长为1,粗线画出的是某几何体的三视图,则该几何体外接球的体积为$8\sqrt{6}π$.
如图,网格纸上的小正方形边长为1,粗线画出的是某几何体的三视图,则该几何体外接球的体积为$8\sqrt{6}π$.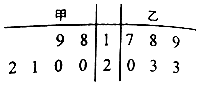 甲、乙两名技工在相同的条件下生产某种零件,连续6天中,他们日加工的合格零件数的统计数据的茎叶图,如图所示.
甲、乙两名技工在相同的条件下生产某种零件,连续6天中,他们日加工的合格零件数的统计数据的茎叶图,如图所示.