题目内容
14.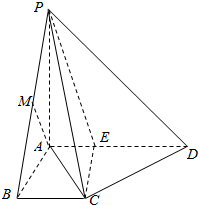 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,BC∥AD,AB⊥AD,PA=AB=BC=1,AD=2.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,BC∥AD,AB⊥AD,PA=AB=BC=1,AD=2.(1)求三棱锥P-ACD的外接球的表面积;
(2)若M为PB的中点,问在AD上是否存在一点E,使AM∥平面PCE?若存在,求$\frac{AE}{ED}$的值;若不存在,说明理由.
分析 (1)根据四棱锥P-ABCD中的垂直关系与数量关系,得出PD是三棱锥P-ACD的外接球直径,由此求出该三棱锥外接球的表面积;
(2)以AB、AD和AP为x、y和z轴,建立空间直角坐标系,利用平面PCE的法向量$\overrightarrow{n}$与$\overrightarrow{AM}$垂直,$\overrightarrow{AM}$•$\overrightarrow{n}$=0,求出$\frac{AE}{ED}$的值,即可得出正确的结论.
解答 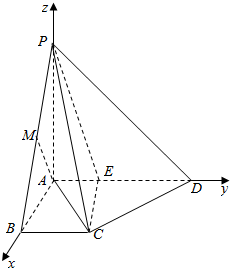 解:(1)四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,BC∥AD,AB⊥AD,PA=AB=BC=1,AD=2;
解:(1)四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,BC∥AD,AB⊥AD,PA=AB=BC=1,AD=2;
∴PD=$\sqrt{{PA}^{2}{+AD}^{2}}$=$\sqrt{{1}^{2}{+2}^{2}}$=$\sqrt{5}$,
AC=$\sqrt{{AB}^{2}{+BC}^{2}}$=$\sqrt{{1}^{2}{+1}^{2}}$=$\sqrt{2}$,
∴PC=$\sqrt{{PA}^{2}{+AC}^{2}}$=$\sqrt{{1}^{2}{+(\sqrt{2})}^{2}}$=$\sqrt{3}$,
CD=$\sqrt{{(\frac{1}{2}AD)}^{2}{+AD}^{2}}$=$\sqrt{{1}^{2}{+1}^{2}}$=$\sqrt{2}$,
∴PC2+CD2=PD2,
∴PC⊥CD;
∴PD是三棱锥P-ACD外接球的直径,
∴该三棱锥外接球的表面积为
S=4π•${(\frac{PD}{2})}^{2}$=π•PD2=5π;
(2)假设线段AD上存在一点E,使AM∥平面PEC,
不妨设$\frac{AE}{ED}$=λ,λ>0,
则$\overrightarrow{AD}$=(1+λ)$\overrightarrow{ED}$,
以AB、AD和AP为x、y和z轴,建立空间直角坐标系,如图所示;
∴$\overrightarrow{AD}$=(0,2,0),
$\overrightarrow{ED}$=$\frac{1}{1+λ}$$\overrightarrow{AD}$=(0,$\frac{2}{1+λ}$,0),
∴$\overrightarrow{AE}$=λ$\overrightarrow{ED}$=(0,$\frac{2λ}{1+λ}$,0);
∴$\overrightarrow{EP}$=(0,-$\frac{2λ}{1+λ}$,1),$\overrightarrow{EC}$=(1,1-$\frac{2λ}{1+λ}$,0),
设平面PCE的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EP}=0}\\{\overrightarrow{n}•\overrightarrow{EC}=0}\end{array}\right.$,
即$\left\{\begin{array}{l}{-\frac{2λ}{1+λ}•y+z=0}\\{x+(1-\frac{2λ}{1+λ})y=0}\end{array}\right.$,
解得$\overrightarrow{n}$=(1,$\frac{λ+1}{λ-1}$,$\frac{2λ}{λ-1}$);
又M($\frac{1}{2}$,0,$\frac{1}{2}$),∴$\overrightarrow{AM}$=($\frac{1}{2}$,0,$\frac{1}{2}$);
当AM∥平面PCE时,$\overrightarrow{AM}$•$\overrightarrow{n}$=0,
∴$\frac{1}{2}$+$\frac{1}{2}$×$\frac{2λ}{λ-1}$=0,
解得λ=$\frac{1}{3}$,
∴$\frac{AE}{ED}$=$\frac{1}{3}$时,AD上存在一点E,使AM∥平面PEC.
点评 本题考查了空间中的平行与垂直关系的应用问题,也考查了空间直角坐标系与法向量的应用问题,
考查了空间想象能力与逻辑推理能力,是综合性题目.

 如图,已知正三棱柱ABC-A1B1C1中,AA1=4,AB=6,点D,E,F分别在棱BB1,CC1,AF上,且BD=C1E=$\frac{1}{2}$AF=1.
如图,已知正三棱柱ABC-A1B1C1中,AA1=4,AB=6,点D,E,F分别在棱BB1,CC1,AF上,且BD=C1E=$\frac{1}{2}$AF=1. 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是梯形,其中AD∥BC,BA⊥AD,AC与BD交于点O,M是AB边上的点,已知PA=AD=4,AB=3,BC=2.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是梯形,其中AD∥BC,BA⊥AD,AC与BD交于点O,M是AB边上的点,已知PA=AD=4,AB=3,BC=2.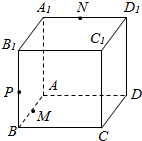 已知M,N,P分别是正方体ABCD-A1B1C1D1的棱,AB,A1D1,BB1上的动点,试过M,N,P三点作正方体ABCD-A1B1C1D1的截面.
已知M,N,P分别是正方体ABCD-A1B1C1D1的棱,AB,A1D1,BB1上的动点,试过M,N,P三点作正方体ABCD-A1B1C1D1的截面.