题目内容
4.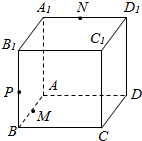 已知M,N,P分别是正方体ABCD-A1B1C1D1的棱,AB,A1D1,BB1上的动点,试过M,N,P三点作正方体ABCD-A1B1C1D1的截面.
已知M,N,P分别是正方体ABCD-A1B1C1D1的棱,AB,A1D1,BB1上的动点,试过M,N,P三点作正方体ABCD-A1B1C1D1的截面.
分析 延长MP交A1B1的延长线于E,连NE交B1C1于F,延长FP交CB的延长线于G,再延长GM交AD于H.则NFPMH就是所要求作的截面.这类题目的解决,关键是找出截面要穿过的棱及其截点.
解答 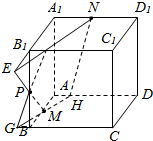 解:作法:
解:作法:
延长MP交A1B1的延长线于E,连NE交B1C1于F,
延长FP交CB的延长线于G,再延长GM交AD于H.
则NFPMH就是所要求作的截面.
证明:
∵E在MP的延长线上,∴N、E、P、M共面.
∵E在A1B1的延长线上,∴E在平面A1B1C1D1上,又N为A1D1的中点,∴NE必与B1C1相交.
∴点F为平面A1B1C1D1、平面B1C1CB、平面MNP的公共点.
∴点F是平面MNP在B1C1上的截点.
∵点F是平面MNP在B1C1上的截点,∴点F在平面MNP上.
而点G在FP的延长线上,∴G在平面MNP上.
∵G在CB的延长线上,∴G在平面ABCD上,又M是AB的中点,∴GM的延长线必与AD相交.
∴点H为平面ABCD、平面AA1D1D、平面MNP的公共点.
∴点H是平面MNP在AD上的截点.
∴NFPMH为所要求作的截面.
点评 本题考查满足条件的正方体的截面的作法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
12.设函数f(x)=ax3+bx2+cx+d(a≠0),已知关于x的五个方程及其相异实根个数如下表所示:
若α为关于f(x)的极大值﹐下列选项中正确的是( )
| 方程 | 根的个数 | 方程 | 根的个数 |
| f(x)-5=0 | 1 | f(x)+4=0 | 3 |
| f(x)-3=0 | 3 | f(x)+6=0 | 1 |
| f(x)=0 | 3 |
| A. | -6<a<-4 | B. | -4<a<0 | C. | 0<a<3 | D. | 3<a<5 |
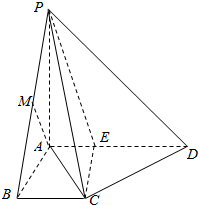 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,BC∥AD,AB⊥AD,PA=AB=BC=1,AD=2.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,BC∥AD,AB⊥AD,PA=AB=BC=1,AD=2.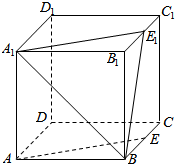 在棱长为1的正方体ABCD-A1B1C1D1中,E、E1分别是BC和B1C1中点,则:
在棱长为1的正方体ABCD-A1B1C1D1中,E、E1分别是BC和B1C1中点,则: