题目内容
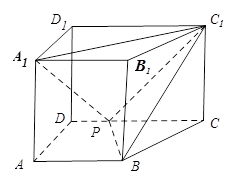
在四棱锥P-ABCD中,侧面PCD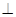 底面ABCD,PD
底面ABCD,PD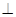 CD,底面ABCD是直角梯形,AB∥DC,
CD,底面ABCD是直角梯形,AB∥DC,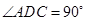 ,
,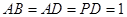 ,
,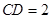 .
.
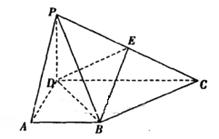
(1)求证:BC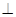 平面PBD:
平面PBD:
(2)求直线AP与平面PDB所成角的正弦值;
(3)设E为侧棱PC上异于端点的一点,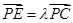 ,试确定
,试确定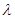 的值,使得二面角E-BD-P的余弦值为
的值,使得二面角E-BD-P的余弦值为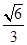 .
.
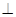 底面ABCD,PD
底面ABCD,PD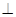 CD,底面ABCD是直角梯形,AB∥DC,
CD,底面ABCD是直角梯形,AB∥DC,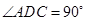 ,
,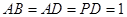 ,
,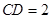 .
.
(1)求证:BC
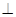 平面PBD:
平面PBD:(2)求直线AP与平面PDB所成角的正弦值;
(3)设E为侧棱PC上异于端点的一点,
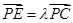 ,试确定
,试确定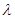 的值,使得二面角E-BD-P的余弦值为
的值,使得二面角E-BD-P的余弦值为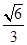 .
.(1)参考解析;(2) ;(3)
;(3)
 ;(3)
;(3)
试题分析:(1)由PD
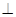 CD,底面ABCD是直角梯形,如图建立空间直角坐标系,
CD,底面ABCD是直角梯形,如图建立空间直角坐标系,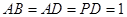 ,
,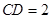 ,写出点D,B,C,P,的坐标,分别写出相应的向量,即可得向量BD与向量CB的数量积为零,向量PD与向量BC的数量积为零.由向量关系转化为空间线面中位置关系,即可得到结论.
,写出点D,B,C,P,的坐标,分别写出相应的向量,即可得向量BD与向量CB的数量积为零,向量PD与向量BC的数量积为零.由向量关系转化为空间线面中位置关系,即可得到结论.(2)要求直线AP与平面PDB所成角的正弦值,等价于求出平面PBD的法向量与向量AP所成的角余弦值即可.
(3)要使得二面角E-BD-P的余弦值为
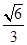 ,关键是求出平面EBD的法向量,由于平面PBD的法向量已知,再通过两法向量的夹角的绝对值等于
,关键是求出平面EBD的法向量,由于平面PBD的法向量已知,再通过两法向量的夹角的绝对值等于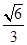 .即可解出
.即可解出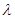 的值.
的值.试题解析:(1)证明:因为侧面
 ⊥底面
⊥底面 ,
, ⊥
⊥ ,
,
所以
 ⊥底面
⊥底面 ,所以
,所以 ⊥
⊥ .
.又因为
 =
= ,即
,即 ⊥
⊥ ,
,以
 为原点建立如图所示的空间直角坐标系,
为原点建立如图所示的空间直角坐标系,则
 ,
, ,
, ,
, ,
,所以

所以
 ,所以
,所以 .
.由
 ⊥底面
⊥底面 ,可得
,可得 ,
,又因为
 ,所以
,所以 ⊥平面
⊥平面 .
.(2)由(1)知平面
 的一个法向量为
的一个法向量为 ,
,
所以

设直线AP与平面PDB所成角为
 ,则
,则
(3)因为
 ,又
,又 ,设
,设
则

所以
 ,
, .设平面
.设平面 的法向量为
的法向量为 ,
,因为
 ,由
,由 ,
, ,
,得
 ,令
,令 ,则可得平面
,则可得平面 的一个法向量为
的一个法向量为 所以
所以 ,
,解得
 或
或 ,又由题意知
,又由题意知 ,故
,故 .
.
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
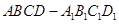 底面
底面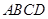 直角梯形,
直角梯形,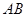 ∥
∥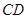 ,
,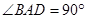 ,
,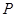 是棱
是棱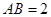 ,
,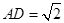 ,
,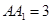 ,
,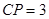 ,
,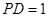 .
.
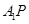 与
与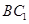 所成的角;
所成的角;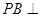 平面
平面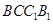 .
.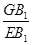 中,已知
中,已知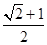 ,
,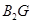 ,
,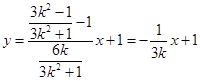 .
.
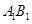 与
与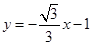 夹角的余弦值;
夹角的余弦值;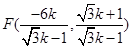 平面角的余弦值.
平面角的余弦值.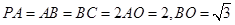 .
.
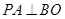 ;
;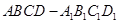 中,底面
中,底面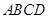 和侧面
和侧面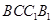 都
都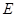 是
是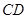 的中点,
的中点,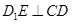 ,
,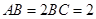 .
.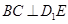
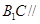 平面
平面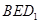 ;
;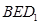 所成的锐二面角的大小为
所成的锐二面角的大小为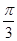 ,求线段
,求线段 的长度.
的长度.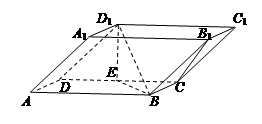

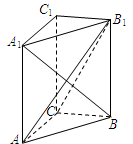
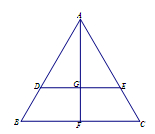
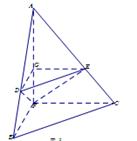
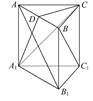
 沿AF折起,得到如图所示的三棱锥
沿AF折起,得到如图所示的三棱锥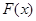 ,其中
,其中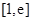 .
.
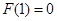 //平面
//平面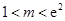 ;
;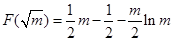 ;
;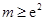 时,求三棱锥
时,求三棱锥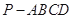 中,侧面
中,侧面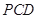
 底面
底面 ,
,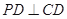 ,底面
,底面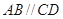 ,
,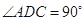 ,
,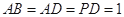 ,
,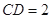 .
.
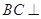 平面
平面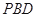 ;
;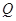 为侧棱
为侧棱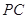 上一点,
上一点,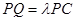 ,试确定
,试确定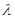 的值,使得二面角
的值,使得二面角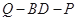 为
为 .
.
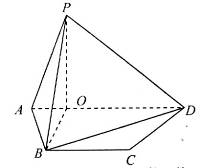
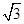 的正三角形,点S在底面ABC上的射影O恰是AC的中点,侧棱SB和底面成45°角.
的正三角形,点S在底面ABC上的射影O恰是AC的中点,侧棱SB和底面成45°角.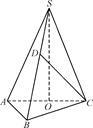
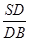 为何值时,CD⊥AB;
为何值时,CD⊥AB;