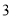题目内容
(本小题满分13分)已知函数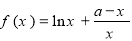 ,其中
,其中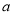 为常数,且
为常数,且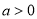 .
.
(1)若曲线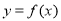 在点
在点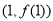 处的切线与直线
处的切线与直线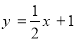 垂直,求
垂直,求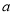 的值;
的值;
(2)若函数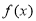 在区间
在区间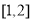 上的最小值为
上的最小值为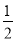 ,求
,求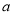 的值.
的值.
(1)3;(2)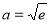 .
.
【解析】
试题分析:(1)由题意,求导得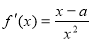 ,由导数的几何意义可得曲线
,由导数的几何意义可得曲线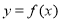 在点
在点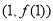 处的切线斜率为
处的切线斜率为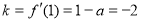 ,从而得到
,从而得到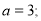 (2)为了研究函数在区间
(2)为了研究函数在区间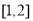 上的最值问题,应研究函数在此区间的单调性,为此应对
上的最值问题,应研究函数在此区间的单调性,为此应对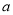 分三种情况讨论:当
分三种情况讨论:当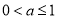 时、当
时、当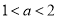 时、当
时、当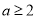 时,在以上三种情况下分别研究导数值的正负,进而确定函数的单调性,求出函数的最小值,
时,在以上三种情况下分别研究导数值的正负,进而确定函数的单调性,求出函数的最小值,
①当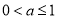 时,
时,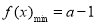
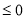 ,不符合题意; ②当
,不符合题意; ②当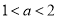 时
时 ,令
,令 ,得
,得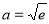 ;③当
;③当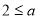 时,
时,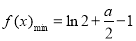
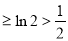 ,不符合题意,因此
,不符合题意,因此 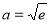 .
.
试题解析: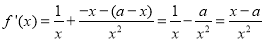 (
(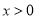 ) 2分
) 2分
(1)因为曲线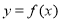 在点(1,
在点(1,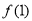 )处的切线与直线
)处的切线与直线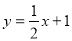 垂直,
垂直,
所以 ,即
,即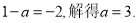 4分
4分
(2)当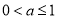 时,
时,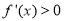 在(1,2)上恒成立,这时
在(1,2)上恒成立,这时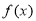 在[1,2]上为增函数,
在[1,2]上为增函数,
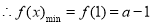 . 6分
. 6分
当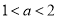 时,由
时,由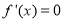 得,
得, ,
,
 对于
对于 有
有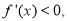
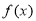 在[1,a]上为减函数,
在[1,a]上为减函数,
对于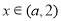 有
有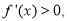
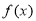 在[a,2]上为增函数,
在[a,2]上为增函数,
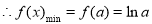 . 8分
. 8分
当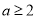 时,
时,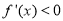 在(1,2)上恒成立,这时
在(1,2)上恒成立,这时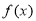 在[1,2]上为减函数,
在[1,2]上为减函数,
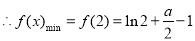 9分
9分
于是,①当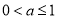 时,
时,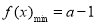
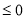 ,不符合题意; 10分
,不符合题意; 10分
②当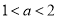 时,
时, ,令
,令 ,得
,得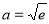 ; 11分
; 11分
③当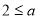 时,
时,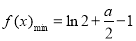
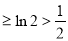 ,不符合题意. 12分
,不符合题意. 12分
综上所述,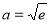 . 13分
. 13分
考点:1、导数的几何意义;2、函数的单调性与导数正负的关系;3、应用导数求最值问题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 是
是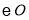 的直径,
的直径,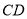 是
是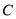 为切点,
为切点,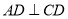 ,交
,交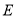 ,连接
,连接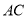 、
、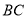 、
、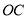 、
、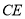 ,延长
,延长 交
交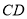 于
于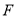 .
.
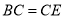 ;
;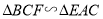 .
. ,
, ,则
,则 的值为( )
的值为( ) B.
B.  C.
C. D.
D.
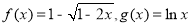 ,对于任意
,对于任意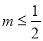 ,都存在
,都存在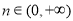 ,使得
,使得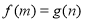 ,则
,则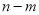 的最小值为( )
的最小值为( )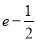 B.
B. 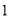 C.
C.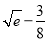 D.
D.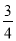
 ,
, ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
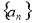 满足
满足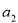 =5,且其前
=5,且其前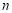 项和
项和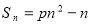 .
.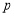 的值和数列
的值和数列 为等比数列,公比为
为等比数列,公比为 ,且其前
,且其前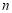 项和
项和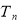 满足
满足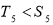 ,求
,求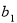 的取值范围.
的取值范围. 若关于x的方程
若关于x的方程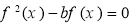 恰有三个不同的实数解,则实数b的取值范围是( ).
恰有三个不同的实数解,则实数b的取值范围是( ). 满足
满足 ,向量
,向量 .若
.若 ,则实数m的最小值为 .
,则实数m的最小值为 .
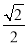 B.
B.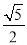 C.
C.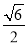 D.
D.