题目内容
12.已知函数f(x)=x4cosx+mx2+x(m∈R),若其导函数f′(x)在区间[-2,2]上有最大值为9,则导函数f′(x)在区间[-2,2]上的最小值为( )| A. | -5 | B. | -7 | C. | -9 | D. | -11 |
分析 先求导数,然后分析发现导数是由一个奇函数和常数的和,然后利用函数的奇偶性容易解决问题.
解答 解:∵f(x)=x4cosx+mx2+x(m∈R),
∴由已知得f′(x)=4x3cosx-x4sinx+2mx+1,
令g(x)=4x3cosx-x4sinx+2mx,则g(x)是奇函数,
由f′(x)的最大值为9,知:g(x)的最大值为8,最小值为-8,
从而f′(x)的最小值为-8+1=-7.
故选:B.
点评 本题考查函数的最小值的求法,是中档题,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
20.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
算得,K2≈7.81.参照附表,得到的正确结论是( )
| 男 | 女 | |
| 爱好 | 40 | 20 |
| 不爱好 | 20 | 30 |
| A. | 再犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关” | |
| B. | 再犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关” | |
| C. | 有99%以上的把握认为“爱好该项运动与性别无关” | |
| D. | 有99%以上的把握认为“爱好该项运动与性别有关”. |
7.如果命题p(n)对n=k成立,则它对n=k+2也成立,若p(n)对n=2成立,则下列结论正确的是( )
| A. | p(n)对所有正整数n都成立 | B. | p(n)对所有正偶数n都成立 | ||
| C. | p(n)对大于或等于2的正整数n都成立 | D. | p(n)对所有自然数都成立 |
 ”是“函数
”是“函数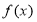 是奇函数”的充要条件
是奇函数”的充要条件 ,则
,则 ”的否命题是“若
”的否命题是“若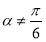 ,则
,则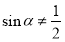 ”
”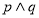 为假命题,则
为假命题,则 均为假命题
均为假命题 ,
, ,则
,则