题目内容
1.在△ABC中,内角A,B,C的对边分别为a,b,c,且3cosAcosB+1=3sinAsinB+cos2C.(1)求C
(2)若△ABC的面积为5$\sqrt{3}$,b=5,求sinA.
分析 (1)移项,利用两角和的余弦函数公式,三角形内角和定理,二倍角的余弦函数公式,诱导公式化简已知可得2cos2C+3cosC-2=0,进而解得cosC,结合范围0<C<π,即可得解C的值.
(2)由已知利用三角形面积公式可求a,由余弦定理可得c的值,进而利用正弦定理即可解得sinA的值.
解答 (本题满分为12分)
解:(1)∵3cosAcosB+1=3sinAsinB+cos2C,
∴3(cosAcosB-sinAsinB)+1=cos2C,
可得:3cos(A+B)+1=cos2C,…2分
∴-3cosC+1=2cos2C-1,
可得:2cos2C+3cosC-2=0,…4分
可得:(2cosC-1)(cosC+2)=0,
∴解得:cosC=$\frac{1}{2}$或cosC=-2(舍去),…5分
∵0<C<π,
∴C=$\frac{π}{3}$…6分
(2)∵S△ABC=$\frac{1}{2}$absinC=5$\sqrt{3}$,b=5,C=$\frac{π}{3}$,可得:a=4,…8分
∵由余弦定理可得:c2=a2+b2-2abcosC=16+25-2×$4×5×\frac{1}{2}$=21,可得:c=$\sqrt{21}$,…10分
∴由正弦定理可得:sinA=$\frac{asinC}{c}$=$\frac{4×\frac{\sqrt{3}}{2}}{\sqrt{21}}$=$\frac{2\sqrt{7}}{7}$…12分
点评 本题主要考查了两角和的余弦函数公式,三角形内角和定理,二倍角的余弦函数公式,诱导公式,三角形面积公式,余弦定理,正弦定理在解三角形中的应用,考查了转化思想,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 的定义域为
的定义域为 ,值域为
,值域为 ,则实数
,则实数 的取值范围是 .
的取值范围是 .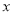 标记.
标记.