题目内容
18.在正项数列{an}中,a1=2,且点($\sqrt{a_n}$,$\sqrt{{a_{n-1}}}$)在直线x-$\sqrt{2}$y=0上,则前n项和Sn等于( )| A. | 2n-1 | B. | 2n+1-2 | C. | ${2^{\frac{n}{2}}}-\sqrt{2}$ | D. | ${2^{\frac{n-2}{2}}}-\sqrt{2}$ |
分析 把点的坐标代入直线方程,求出an与an+1的关系,判断数列的特征,即可求解前n项和.
解答 解:因为点($\sqrt{a_n}$,$\sqrt{{a_{n-1}}}$)在直线x-$\sqrt{2}$y=0上,
所以$\sqrt{a_n}$-$\sqrt{2}$×$\sqrt{{a_{n-1}}}$=0,即an=2an-1,
所以数列{an}是首项为2,公比为2的等比数列.
它的前n项和为:Sn=$\frac{2(1-{2}^{n})}{1-2}$=2n+1-2.
故选B.
点评 本题考查等比数列的前n项和的求法,等比数列的判断,考查计算能力.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
9.设函数f(x)=-4x+2x+1-1,g(x)=lg(ax2-4x+1),若对任意x1∈R,都存在x2∈R,使f(x1)=g(x2),则实数a的取值范围为( )
| A. | (0,4] | B. | (-∞,4] | C. | (-4,0] | D. | [4,+∞) |
10.执行如图所示的程序框图,若输出的S=183,则判断框内应填入的条件是( )
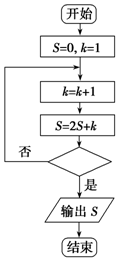

| A. | k>7? | B. | k>6? | C. | k>5? | D. | k>4? |
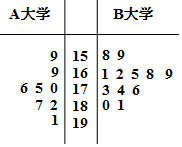 某市旅游节需在A大学和B大学中分别招募8名和12名志愿者,这20名志愿者的身高(单位:cm)绘制出如图所示的茎叶图.若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有B大学的“高个子”才能担任“兼职导游”.
某市旅游节需在A大学和B大学中分别招募8名和12名志愿者,这20名志愿者的身高(单位:cm)绘制出如图所示的茎叶图.若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有B大学的“高个子”才能担任“兼职导游”.