题目内容
3.下列四组函数中,表示为同一函数的是( )| A. | f(x)=$\frac{{x}^{2}-1}{x-1}$,g(x)=x+1 | B. | y=x0与g(x)=$\frac{1}{{x}^{0}}$ | ||
| C. | f(x)=|x|,g(x)=$\sqrt{{x}^{2}}$ | D. | f(x)=$\sqrt{x+1}$•$\sqrt{x-1}$,g(x)=$\sqrt{{x}^{2}-1}$ |
分析 根据两个函数是同一个函数的定义,函数的三要素均相等,或两个函数的图象一致,根据函数的定义域与函数的解析式一致时,函数的值域一定相同,我们逐一分析四个答案中两个函数的定义域和解析式是否一致,即可得到答案.
解答 解:对于A,$f(x)=\frac{{x}^{2}-1}{x-1}$,(x≠1),g(x)=x+,(x∈R),两个函数的定义域不一致,故A错误;
对于B,y=x0=1与 g(x)=$\frac{1}{{x}^{0}}$=1定义域都是{x|x≠0},但函数解析式不一致,故B错误;
对于C,f(x)=|x|与g(x)=$\sqrt{{x}^{2}}$=|x|,且两个函数的定义域均为R,故C正确;
对于D,f(x)=$\sqrt{x+1}$•$\sqrt{x-1}$,(x≥1),g(x)=$\sqrt{{x}^{2}-1}$,(x≥1或x≤-1),两函数的定义域不同,不为同一函数,故D错误.
∴四组函数中,表示为同一函数的是:C.
故选:C.
点评 本题考查的知识点是判断两个函数是否为同一函数,熟练掌握判断两个函数是否为同一函数的方法,正确理解两个函数表示同一函数的概念是解答本题的关键,是中档题.

练习册系列答案
相关题目
11.下面的伪代码输出的结果S为( )
I←1
While I<8
I←I+2
S←2I+3
End while
Print S.
I←1
While I<8
I←I+2
S←2I+3
End while
Print S.
| A. | 17 | B. | 19 | C. | 21 | D. | 23 |
12.已知三角形ABC内的一点D满足$\overrightarrow{DA}$•$\overrightarrow{DB}$=$\overrightarrow{DB}$•$\overrightarrow{DC$=$\overrightarrow{DC}$•$\overrightarrow{DA}$=-2,且|$\overrightarrow{DA}$|=|$\overrightarrow{DB}$|=|$\overrightarrow{DC}$|.平面ABC内的动点P,M满足|$\overrightarrow{AP}$|=1,$\overrightarrow{PM}$=$\overrightarrow{MC}$,则|$\overrightarrow{BM}$|2的最大值是( )
| A. | $\frac{49}{4}$ | B. | $\frac{43}{4}$ | C. | $\frac{{37+6\sqrt{3}}}{4}$ | D. | $\frac{{37+2\sqrt{33}}}{4}$ |
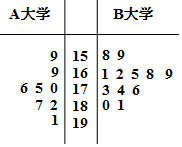 某市旅游节需在A大学和B大学中分别招募8名和12名志愿者,这20名志愿者的身高(单位:cm)绘制出如图所示的茎叶图.若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有B大学的“高个子”才能担任“兼职导游”.
某市旅游节需在A大学和B大学中分别招募8名和12名志愿者,这20名志愿者的身高(单位:cm)绘制出如图所示的茎叶图.若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有B大学的“高个子”才能担任“兼职导游”.