题目内容
11.设函数y=$\frac{x+3}{x-4}$和y=$\frac{(x-3)(x+3)}{{x}^{2}-7x+12}$的值域分别为A和B,则( )| A. | A=B | B. | A?B | C. | A?B | D. | A∪B=R |
分析 根据分式函数的性质先求出函数的值域,然后根据集合的基本关系进行判断即可.
解答 解:y=$\frac{x+3}{x-4}$=$\frac{x-4+7}{x-4}$=1-$\frac{7}{x-4}$≠1,即函数的值域为A={x|x≠1},
y=$\frac{(x-3)(x+3)}{{x}^{2}-7x+12}$=$\frac{(x-3)(x+3)}{(x-3)(x-4)}$=$\frac{x+3}{x-4}$=$\frac{x-4+7}{x-4}$=1-$\frac{7}{x-4}$≠1,函数的定义域为{x|x≠3且x≠4},
当x=3时,y=$\frac{3+3}{3-4}$=-6,即函数的值域B={x|x≠1且x≠-6},
则B?A,
故选:B.
点评 本题主要考查函数值域的计算以及集合关系的判断,根据分式函数的性质是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.在△ABC中,如果(b+c+a)(b+c-a)=bc,那么A等于( )
| A. | 30° | B. | 120° | C. | 60° | D. | 150° |
2.已知函数f(2x+1)=4x2+4x-5,则f(3)=( )
| A. | 43 | B. | -3 | C. | 2 | D. | 3 |
6.把45化为二进制数为( )
| A. | 1011112 | B. | 1011012 | C. | 1101012 | D. | 1111012 |
3.某几何体的三视图如图所示,则该几何体的表面积是( )
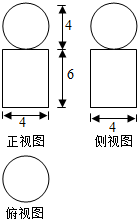

| A. | 44π | B. | 48π | C. | $\frac{116π}{3}$ | D. | $\frac{128π}{3}$ |
20.不等式|2x-1|≤7的解集是( )
| A. | {x|x≥-3} | B. | {x|x≤4} | C. | {x|-3≤x≤4} | D. | {x|x≤-3或x≥4} |