题目内容
【题目】如图,在平面直角坐标系xOy中,已知![]() 为椭圆
为椭圆![]() 的上顶点,P为椭圆E上异于上、下顶点的一个动点.当点P的横坐标为
的上顶点,P为椭圆E上异于上、下顶点的一个动点.当点P的横坐标为![]() 时,
时,![]() .
.
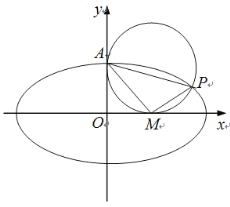
(1)求椭圆E的标准方程;
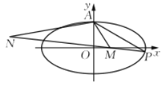
(2)设M为x轴的正半轴上的一个动点.
①若点P在第一象限内,且以AP为直径的圆恰好与x轴相切于点M,求AP的长.
②若![]() ,是否存在点N,满足
,是否存在点N,满足![]() ,且AN的中点恰好在椭圆E上?若存在,求点N的坐标;若不存在,请说明理由.
,且AN的中点恰好在椭圆E上?若存在,求点N的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②存在点
;②存在点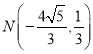 满足题意.
满足题意.
【解析】
(1)根据题意可知![]() ,可求出P点坐标,代入方程求出
,可求出P点坐标,代入方程求出![]() 即可;
即可;
(2)①设![]() ,则可表示出圆心坐标可设为
,则可表示出圆心坐标可设为![]() ,
,![]() ,根据圆的性质
,根据圆的性质![]() 及点P在椭圆上列出方程组求解即可;
及点P在椭圆上列出方程组求解即可;
②设![]() ,
,![]() ,根据
,根据![]() , AN的中点恰好在椭圆E上,且
, AN的中点恰好在椭圆E上,且![]() 得到
得到![]() 点坐标,即可求解.
点坐标,即可求解.
(1)因为![]() 是椭圆E的上顶点,所以
是椭圆E的上顶点,所以![]() .
.
当点P的横坐标为![]() 时,
时,![]() .
.
设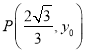 ,则
,则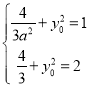 ,解得
,解得 ,
,
所以椭圆E的标准方程为![]() .
.
(2)①设![]() ,则以AP为直径的圆的圆心坐标可设为
,则以AP为直径的圆的圆心坐标可设为![]() .
.
又因为![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() ,
,
得![]() .
.
因为点P在椭圆E上,所以![]() ,
,
与![]() 联立解得
联立解得 (负值舍去),
(负值舍去),
所以![]() .
.
②设![]() ,
,![]() .
.
因为![]() ,
,
所以![]() ,
,
解得![]() ,
,
所以AN的中点坐标为![]()
因为AN的中点在椭圆E上,
所以![]() .(*)
.(*)
因为![]() ,所以
,所以![]() .
.
因为点P在椭圆E上,
所以![]() ,(**)
,(**)
与![]() 联立消去
联立消去![]() 得
得
![]() .
.
又因为![]() ,所以
,所以![]() ,
,
代入(*)式和(**)式得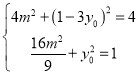
消去m得![]() .
.
又因为![]() .所以
.所以![]() ,
,
代入(**)式和![]() ,
,
解得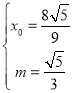 (负值舍去),
(负值舍去),
故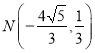 .
.
综上,存在点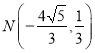 ,满足
,满足![]()
且AN的中点恰好在椭圆E上.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目