题目内容
17. 如图,在四棱锥P-ABCD中,底面ABCD为边长为2的菱形,∠DAB=60°,△PAD为正三角形,PB=$\sqrt{6}$.
如图,在四棱锥P-ABCD中,底面ABCD为边长为2的菱形,∠DAB=60°,△PAD为正三角形,PB=$\sqrt{6}$.(1)证明:平面PAD⊥平面ABCD;
(2)E为线段PB上的点,平面PAD与平面ACE所成锐二面角为30°,$\overrightarrow{PE}$=λ$\overrightarrow{PB}$,求出λ的值.
分析 (1)由底面ABCD为菱形,且E为AD中点,∠DAB=60°,可得PF=BF=$\sqrt{3}$,可得PB2=PF2+BF2,PF⊥BF,即平面PAD⊥平面ABCD;
(2)建立空间直角坐标系,则A(1,0,0),C(-2,$\sqrt{3}$,0),P(0,0,$\sqrt{3}$),E(0,$\sqrt{3}λ$,$\sqrt{3}-\sqrt{3}λ$),求出平面ABCD和PAD的法向量,即可求解.
解答 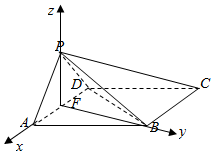 (1)证明:取AD中点F,连接PF,FB,∵底面ABCD为边长为2的菱形,△PAD为正三角形,∴PF⊥AD,PF=$\sqrt{3}$
(1)证明:取AD中点F,连接PF,FB,∵底面ABCD为边长为2的菱形,△PAD为正三角形,∴PF⊥AD,PF=$\sqrt{3}$
∵∠DAB=60°,△PAD为正三角形,∴BF⊥AD,BF=$\sqrt{3}$
∵$PB=\sqrt{6}$,∴PB2=PF2+BF2,∴PF⊥BF,
∴BF⊥面ABCD,即平面PAD⊥平面ABCD;
(2)如图建立空间直角坐标系,则A(1,0,0),C(-2,$\sqrt{3}$,0),P(0,0,$\sqrt{3}$),E(0,$\sqrt{3}λ$,$\sqrt{3}-\sqrt{3}λ$)
设平面ABCD的法向量为$\overrightarrow{n}=(x,y,z)$,$\overrightarrow{AC}=(-3,\sqrt{3},0)$,$\overrightarrow{AE}=(-1,\sqrt{3}λ,\sqrt{3}-\sqrt{3}λ)$
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AC}=-3x+\sqrt{3}y=0}\\{\overrightarrow{n}•\overrightarrow{AE}=-x+\sqrt{3}λy+\sqrt{3}(1-λ)z=0}\end{array}\right.$,可得$\overrightarrow{n}$=(1,$\sqrt{3}$,$,\frac{1-3λ}{\sqrt{3}(1-λ)}$)
易得平面PAD的法向量为$\overrightarrow{m}=(0,1,0)$
cos30°=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{\sqrt{3}}{1×\sqrt{1+3+(\frac{1-3λ}{\sqrt{3}(1-λ)})^{2}}}=\frac{\sqrt{3}}{2}$,
解得$λ=\frac{1}{3}$.
点评 本题考查了面面垂直的判定,及向量法求二面角,属于中档题.

| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
 如图所示的是下列几个函数的图象:①y=ax; ②y=bx; ③y=cx; ④y=dx.则a,b,c,d与0和1的关系是( )
如图所示的是下列几个函数的图象:①y=ax; ②y=bx; ③y=cx; ④y=dx.则a,b,c,d与0和1的关系是( )| A. | 0<a<b<1<c<d | B. | 0<b<a<1<d<c | C. | 0<b<a<1<c<d | D. | 1<a<b<c<d |
| A. | 1+i | B. | 1-i | C. | 2i | D. | -2i |
| 身高x(cm) | 160 | 165 | 170 | 175 | 180 |
| 身高y(kg) | 63 | 66 | 70 | 72 | 74 |
| A. | 70.09 | B. | 70.12 | C. | 70.55 | D. | 71.05 |
| A. | 减函数 | |
| B. | 增函数 | |
| C. | 在(-2,-1)内为增函数.在(-1,0)内为减函数 | |
| D. | 以上都不对 |
 函数f(x)=2sin(ωx+φ)(ω>0,$-\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则ω=2.
函数f(x)=2sin(ωx+φ)(ω>0,$-\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则ω=2.