题目内容
(本小题满分12分)设向量 ,其中
,其中 ,
, ,已知函数
,已知函数 的最小正周期为
的最小正周期为 .
.
(1)求 的对称中心;
的对称中心;
(2)若 是关于
是关于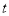 的方程
的方程 的根,且
的根,且 ,求
,求 的值.
的值.
【答案】(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)先利用两角和与差的正弦化简函数的解析式,再根据函数最小正周期求得函数的解析式,由此求得函数的对称中心;(2)先根据方程根的概念求得 的值,再由
的值,再由 的范围求得
的范围求得 的值,从而代入函数解析式中求得
的值,从而代入函数解析式中求得 的值.
的值.
试题解析:(1) 

又  , 得
, 得  所以
所以  对称中心为
对称中心为 
(2)由 得
得  或
或  即
即 或
或 ,又
,又
所以 ,得
,得 ,故
,故
考点:1、两角两角和与差的正弦;2、三角函数的周期;3、特殊三角形函数的值.
【规律点睛】平面向量与三角函数的综合,通常利用平面向量的垂直、平行、数量积公式等知识将向量问题转化为三角函数问题,再结合三角知识求解.而求三角函数的最值(值域)、单调性、奇偶性、对称性,通常要将函数的解析式转化为 的形式,然后利用整体思想求解.
的形式,然后利用整体思想求解.
【题型】解答题
【适用】较难
【标题】【百强校】2016届江西省临川一中高三上学期期中文科数学试卷(带解析)
【关键字标签】
【结束】
(本小题满分12分)在四棱柱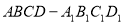 中,
中, ,底面
,底面 为菱形,
为菱形,
 ,已知
,已知 .
.

(1)求证:平面 平面
平面 ;
;
(2)求点 到平面
到平面 的距离.
的距离.
练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目


 是增函数,无极值;②
是增函数,无极值;② 上没有最大值;③函数
上没有最大值;③函数 存在与直线
存在与直线 平行的切线,则实数
平行的切线,则实数 的取值范围是
的取值范围是 其中正确命题的个数为( )
其中正确命题的个数为( )
 的右焦点是F,左右顶点分别为
的右焦点是F,左右顶点分别为 ,过F作
,过F作 的垂线与双曲线交于B,C两点,若
的垂线与双曲线交于B,C两点,若 ,则该双曲线渐近线的斜率为( )
,则该双曲线渐近线的斜率为( ) B.
B. C.
C. D.
D.
 .
. 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 在区间
在区间 上的最大值.
上的最大值. 对任意实数
对任意实数 都满足
都满足 ,且
,且 .令
.令 .
. 在
在 上的最小值为0,求
上的最小值为0,求 的值;
的值; ,若函数
,若函数 有5个不同的零点,求实数
有5个不同的零点,求实数 的取值范围.
的取值范围. ,若关于
,若关于 的函数
的函数 有
有 个不同的零点,则实数
个不同的零点,则实数 的取值范围是 .
的取值范围是 . 是等差数列,其前
是等差数列,其前 项和为
项和为 ,若首项
,若首项 且
且 ,有下列四个命题:
,有下列四个命题: ;
; ;
; 数列
数列 项和最大;
项和最大; 使
使 的最大
的最大 值为
值为 ;
; 上为增函数的是 ( )
上为增函数的是 ( ) B.
B.
 D.
D.