题目内容
已知数列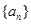 的前
的前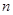 项和为
项和为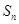 ,常数
,常数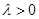 ,且
,且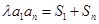 对一切正整数
对一切正整数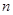 都成立。
都成立。
(Ⅰ)求数列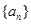 的通项公式;
的通项公式;
(Ⅱ)设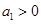 ,
,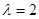 ,求证:
,求证: 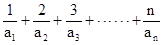 <4
<4
(1)若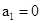 时,
时,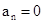 ,若
,若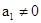 ,则
,则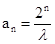
(2)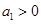 ,
,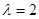 时,
时,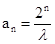 ,设
,设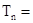
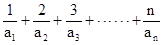 ,结合错位相减法来得到比较。
,结合错位相减法来得到比较。
解析试题分析:(Ⅰ)取n=1得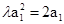 ,
,
若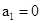 则
则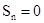 当n》2时,
当n》2时,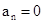 ,
,
若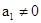 则
则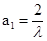 ,所以n》2时,由
,所以n》2时,由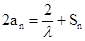 ,
,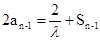 相减得
相减得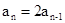 ,所以数列
,所以数列 是等比数列,于是
是等比数列,于是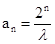 ,
,
综上可知:若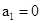 时,
时,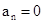 ,若
,若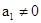 ,则
,则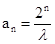
(Ⅱ)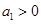 ,
,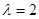 时,
时,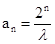 ,设
,设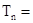
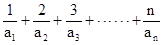 即
即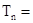

所以,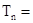 2
2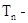
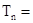
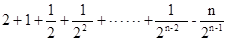
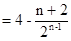 <4
<4
考点:数列的通项公式与前n项和的关系
点评:主要是考查了数列的通项公式求解和错位相减法求和的综合运用,属于基础题。

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
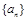 和公比为
和公比为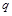
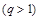 的等比数列
的等比数列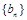 满足:
满足: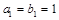 ,
,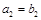 ,
,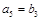 .
.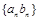 的前
的前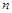 项和为
项和为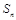 .
.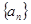 的前
的前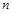 项和
项和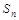 是二项式
是二项式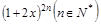 展开式中含
展开式中含 奇次幂的系数和.
奇次幂的系数和.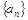 的通项公式;
的通项公式;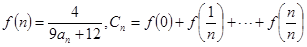 ,求
,求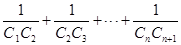 的值.
的值.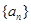 的前
的前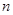 项和为
项和为 ,且
,且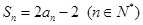 .
.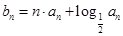 ,数列
,数列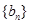 的前
的前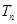 ,若不等式
,若不等式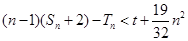 对任意
对任意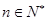 恒成立,求实数
恒成立,求实数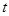 的取值范围.
的取值范围. ,其前
,其前 项和
项和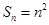 ,数列
,数列 满足
满足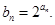
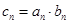 ,求数列
,求数列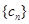 的前
的前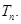
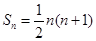
 ,求数列{Cn}的前n项和Tn
,求数列{Cn}的前n项和Tn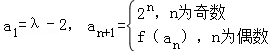 .
.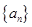 的相邻两项
的相邻两项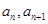 是关于
是关于 的方程
的方程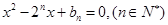 的两根,且
的两根,且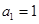 .
.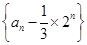 是等比数列;
是等比数列; 项和
项和 ;
;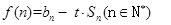 若
若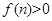 对任意的
对任意的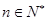 都成立,求
都成立,求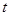 的取值范围。
的取值范围。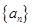 的前n项和为
的前n项和为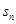 ,满足
,满足
 ,求数列
,求数列 的前n项和
的前n项和 。
。