题目内容
已知数列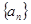 的前
的前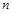 项和
项和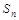 是二项式
是二项式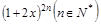 展开式中含
展开式中含 奇次幂的系数和.
奇次幂的系数和.
(1)求数列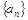 的通项公式;
的通项公式;
(2)设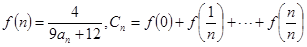 ,求
,求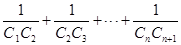 的值.
的值.
(1)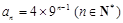 (2)
(2)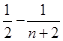
解析试题分析:(1)解:记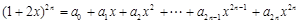
令x = 1得: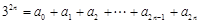
令x =-1得: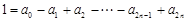
两式相减得: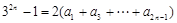 ,∴
,∴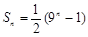 4分
4分
当n≥2时,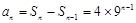
当n = 1时,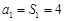 ,适合上式
,适合上式
∴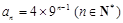 6分
6分
(2)解: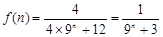
注意到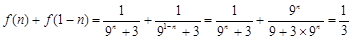 8分
8分 可改写为:
可改写为: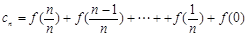
∴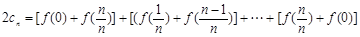
故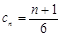 10分
10分
∴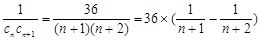
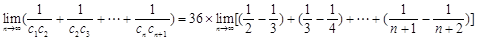 12分
12分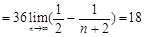 14分
14分
考点:二项式定理和数列
点评:解决的关键是利用二项式定理来得到数列的通项公式,同时利用裂项法求和得到,属于中档题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
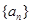 是首项为
是首项为 ,公差为
,公差为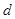 的等差数列(
的等差数列(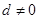 ),
),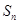 是前
是前 项和. 记
项和. 记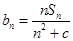 ,
,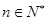 ,其中
,其中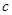 为实数.
为实数.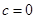 ,且
,且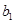 ,
,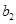 ,
,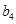 成等比数列,证明:
成等比数列,证明: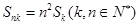 ;
; 是等差数列,证明
是等差数列,证明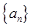 是首项
是首项 的等比数列,且
的等比数列,且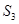 ,
,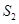 ,
, 成等差数列.
成等差数列.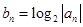 ,设
,设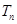 为数列
为数列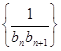 的前
的前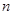 项和,若
项和,若 对一切
对一切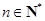 恒
恒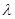 的最小值.
的最小值.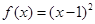 ,数列
,数列 是公差为d的等差数列,
是公差为d的等差数列,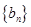 是公比为q(
是公比为q(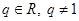 )的等比数列.若
)的等比数列.若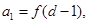
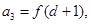

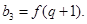
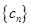 对任意自然数n均有
对任意自然数n均有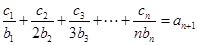 ,求
,求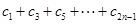 的值;
的值;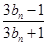 与
与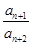 的大小.
的大小.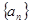 前
前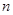 项和
项和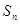 满足
满足 且
且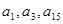 成等比数列,求
成等比数列,求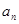 .
.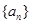 满足
满足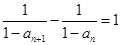 ,且
,且 .
.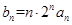 ,求数列
,求数列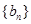 的前
的前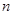 项和
项和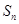 ;
;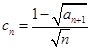 ,记
,记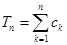 ,证明:
,证明: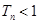 .
. 中,
中, .
. ,求数列
,求数列 的通项公式;
的通项公式; 求证:
求证: .
. 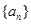 的前
的前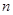 项和为
项和为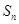 ,常数
,常数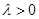 ,且
,且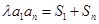 对一切正整数
对一切正整数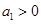 ,
,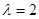 ,求证:
,求证: 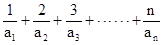 <4
<4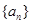 是公差
是公差 的等差数列,
的等差数列, 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且 ,
, .
. …),求数列
…),求数列 的前
的前 项和
项和 .
.